Let’s start!
There are number of applications when linear data structure is not appropriate. Linear structure means we put and get elements in and from linked list, stack, and queue in linear order.
Linked list, stack, and queues are linear data structure. While tree is a non-linear data structure.
As the name indicates we can know that tree data structure will involve root, branches and leaves.
Binary Trees
“Every leaf will have two children in this tree.”
A binary tree is a finite set of elements that is either empty or is partitioned into three disjoint subsets.
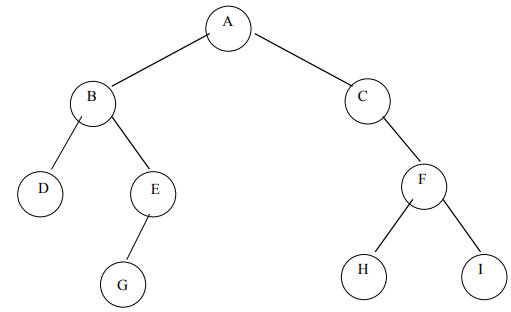
The first subset contains a single element called the root of the tree. The other two subsets are themselves binary trees called the left and right sub-trees.
Each element of a binary tree is called a node of the tree.
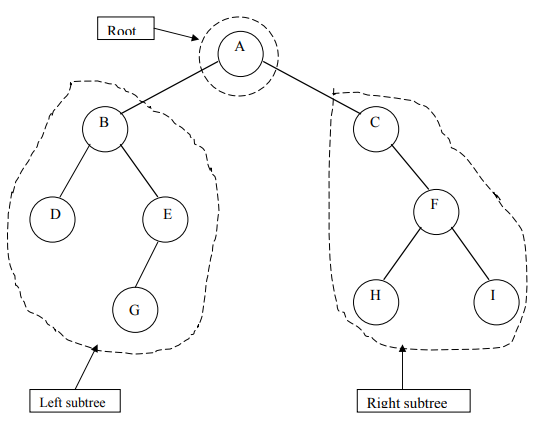
Alright! Nodes connected to each other in such a way that they react like a tree (having root, branches and leaves). Wait! Is that enough to define a tree? Not yet! ☹️
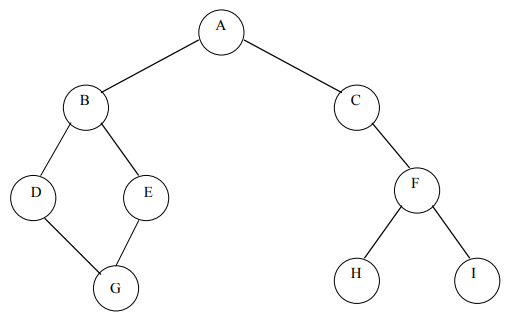
“To reach a node from another node, there should be only one way. This would be called a tree.”
The following image isn’t tree. Because it has multiple ways (from node D or E) to reach node “G”.
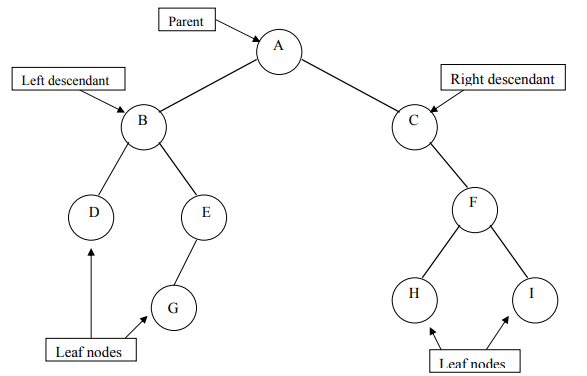
Terminologies of a Binary tree
Strictly Binary Tree
“A binary tree is said to be a strictly binary tree if every non-leaf node in a binary tree has non-empty left and right subtrees.”
See the Fig 5, before adding node “J” and “K”, this tree was not strictly binary, but now, it is.
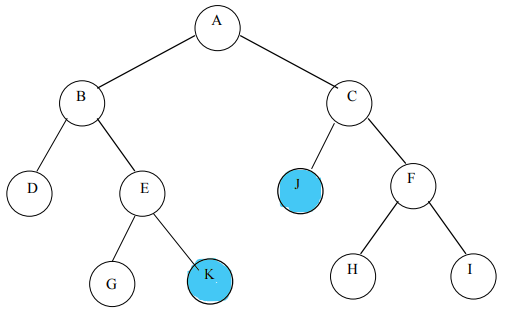
Leaf Nodes are those nodes that have no right and left children.
Non-leaf Nodes are those that have right or left or both children.
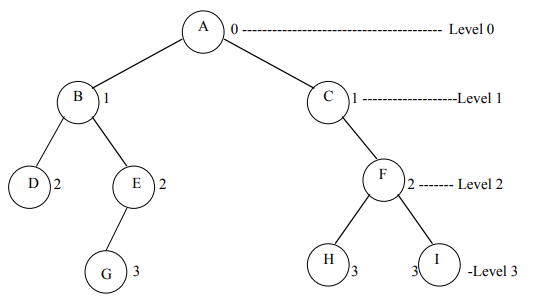
Level
The level of a node in a binary tree is defined as follows:
- Root has level 0.
- Level of any other node is one more than the level its parent (father).
- The depth of a binary tree is the maximum level of any leaf in the tree.
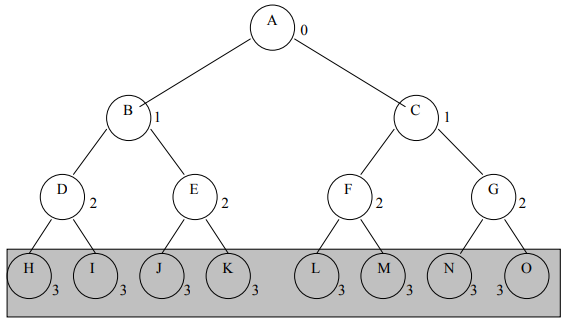
Complete Binary Tree
“A complete binary tree of depth d is the strictly binary tree all of whose leaves are at level d.”
You can see that the leaf nodes are at the same level in Fig 7:
Before you move ahead!
- k = It is the level number of the tree
- d = Depth of the tree
- n = No. of the nodes
REFERENCE: CS301 Handouts (page 108 to 121)
I was recommended this website by my cousin I am not sure whether this post is written by him as nobody else know such detailed about my trouble You are amazing Thanks
I was recommended this website by my cousin I am not sure whether this post is written by him as nobody else know such detailed about my difficulty You are wonderful Thanks
[…] named after two persons Adelson-Velskii and Landis. These two had devised a technique to make the tree […]
This paragraph is telling about the abbreviation of AVL, which is based on the names of 3 scientists, who were involved in giving the idea about AVL tree.
[…] The binary tree serves as a useful structure for making two-way decisions at each point. […]
In binary tree, each node has two children (left child, right child). For traversal, you’ve only two options to go; left or right.