Building the Expression Tree

Let’s Start!

The reason why we need the expression tree is that in case of compilers, when languages are translated into machine language, tree-like data structures are used.

That’s how expression tree looks like:

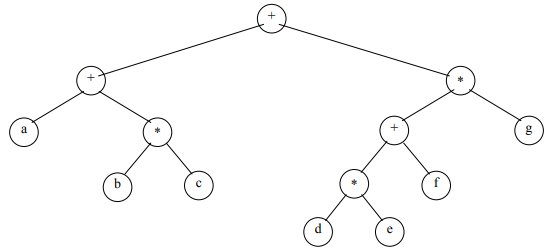
In-order Traversal of the Tree

The in-order traversal of this expression tree in Figure 1 yields the following expression = a+b*c+d*e+f*g

Leaf nodes are operands and inner nodes are operators.

If we want to put the parenthesis in the expression then the following code will help in this regard, which will yield the following expression in return: ( a + ( b * c )) + ((( d * e ) + f ) * g )

void inorder(TreeNode<int>* treeNode){
    if( treeNode != NULL ){
    cout << "(";
    inorder(treeNode->getLeft());
    cout << ")";
    cout << *(treeNode->getInfo());
    cout << "(";
    inorder(treeNode->getRight());
    cout << ")";
    }
}

Post-order of the Tree

Post-order of the expression tree in Figure 1 will yield following expression: a b c * + d e * f + g * +

In post-order, we first print Left, then right and then parent node. And we’ve already discussed this in the Evaluation of Postfix Expression.

Before Building the Expression Tree

Suppose someone is using a spreadsheet program and typed a mathematical expression in the infix form. We will first convert the infix expression into the postfix expression before building expression tree with this postfix expression.

Finally Building the Expression Tree

Let’s see how we can build this tree. We have some mathematical expressions while having binary operators. We want to develop an algorithm to convert postfix expression into an expression tree.

Logic

Logic behind the building of expression tree will be following, but know that this logic will be implemented after the expression has been converted into postfix expression.

• Read the postfix expression from the left to right.
• If the symbol is an operand, put it in a tree node and push it on the stack.
• If symbol is an operator, pop two trees (nodes) from the stack, form the new tree with operator as the root and T1 and T2 as left and right subtrees and push this on the stack.

Understand through Figures

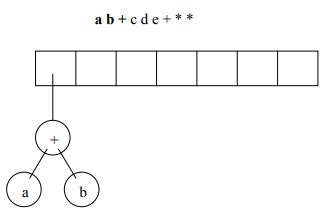
Let’s perform the logic in the form of figures to understand it better. We’ll take the following expression as our example = a b + c d e + * *

Figure 2: If symbol is an operand, put it in a one node tree and push it on a stack.

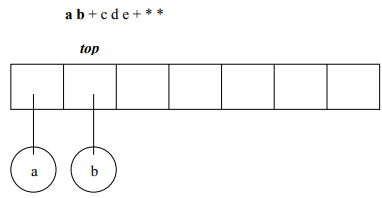
Figure 3: If symbol is an operator, then pop the top two nodes and make them left and right subtree of the node operator. After making their tree, push it back to the stack.

Now, we’ve understood the logical. So, let’s move smoothly. 🙂

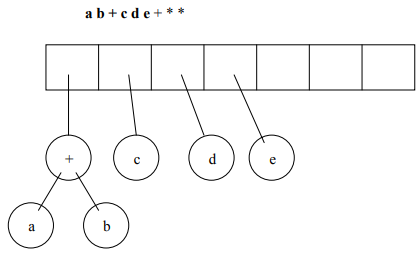
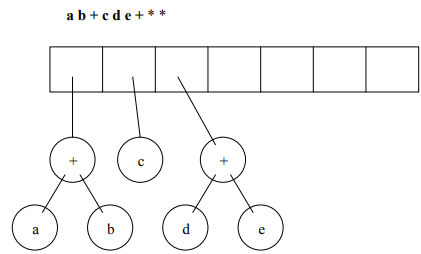
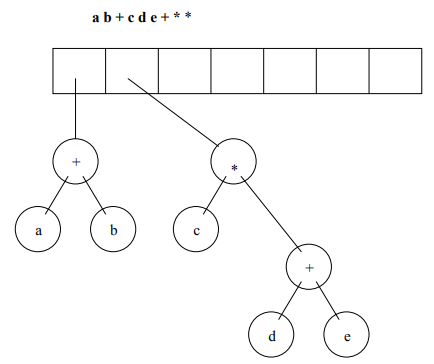
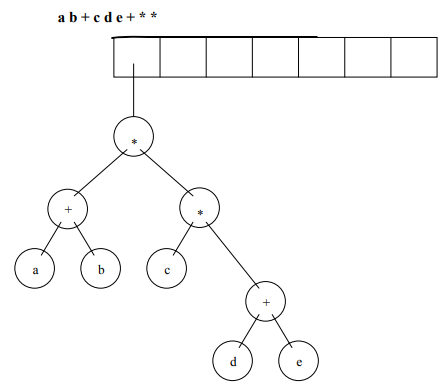
Figure 7 shows our final expression tree.

In the End

This is the way to build an expression tree. We have used the algorithm to convert the infix form into postfix form. We have also used stack data structure. With the help of templates, we can insert any type of data in the stack. We have used the expression tree algorithm and very easily built the expression tree.

REFERENCE: CS301 Handouts (page 284 to 291)