Cases of Rotation in AVL tree

Let’s Start!

As we know that, in Example of Insertion of nodes in AVL tree, the single rotation was not of great help to make the balance of AVL tree!

Here are the four cases of rotation to make BST an AVL tree:

1. An insertion into left subtree of the left child of α. (left-left insertion, outside insertion).
2. An insertion into right subtree of the left child of α.
3. An insertion into left subtree of the right child of α.
4. An insertion into right subtree of the right child of α. (right-right insertion, outside insertion).

NOTE: α is the node whose balance is 2 or -2.

The triangles in the tree are subtrees (having many nodes in it, and we’re not concerned knowing about them).

Outside Rotation

The insertion occurs on the outside (i.e., left-left or right-right) in cases 1 and 4. Single rotation can fix the balance in cases 1 and 4.

Case 1

An insertion into left subtree of the left child of α.

Solution: Single Right Rotation

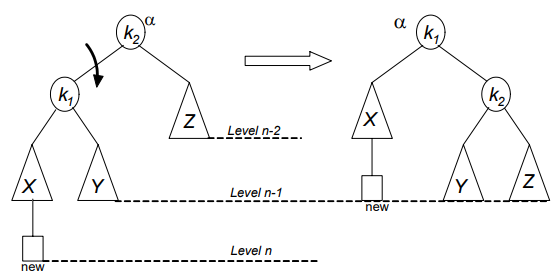
You can see in Fig 1 how we performed Single Right Rotation to make the tree balanced.

C++ Code for Single Right Rotation

TreeNode <int> * SingleRightRotation(TreeNode <int> * k2) {
    if (k2 == NULL) return NULL;
    TreeNode <int> *k1 = k2->getLeft();

    k2->setLeft(k1->getRight());
    k1->setRight(k2);

    int h = MAX(height(k2->getLeft()), height(k2->getRight()));
    k2->setHeight(h + 1);
    h = MAX(height(k1->getLeft()), height(k1->getRight()));
    k1->setHeight(h + 1);
    return k1;
}

Case 4

An insertion into right subtree of the right child of α.

Solution: Single Left Rotation

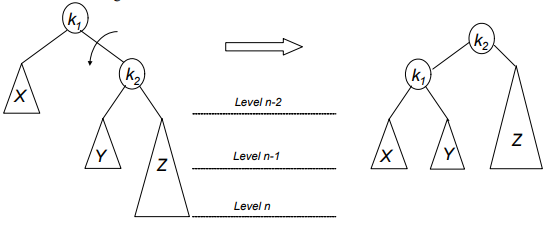
C++ code for Single Left Rotation

TreeNode <int> * SingleLeftRotation(TreeNode <int> *k1) {
    if (k1 == NULL) return NULL;
    TreeNode <int> *k2 = k1->getRight();

    k1->setRight(k2->getLeft());
    k2->setLeft(k1);

    int h = MAX(height(k1->getLeft()), height(h1->getRight()));
    k1->setHeight(h + 1);
    h = MAX(height(k2->getLeft()), height(k2->getRight()));
    k2->setHeight(h + 1);
    return k2;
}

Inner Rotation

Insertion occurs on the inside in cases 2 and 3 which a single rotation cannot fix.

Case 2

An insertion into right subtree of the left child of α.

Solution: Double Left Right Rotation

As the name shows, this rotation involves two rotations.

1. Left Rotation

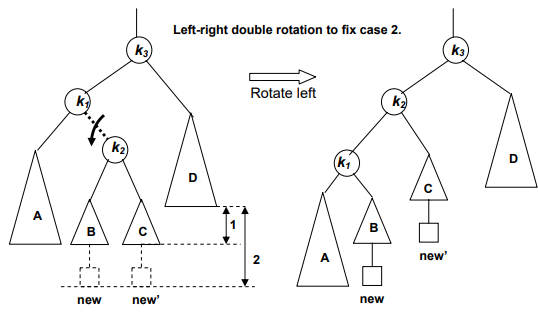
2. Right Rotation

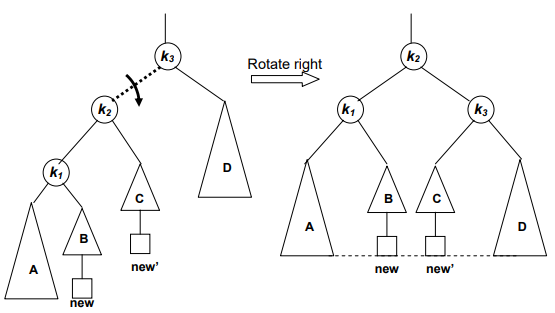
C++ code for Double Left Right Rotation

TreeNode <int> * doubleLeftRightRotation(TreeNode <int> *k3) {
    if (k3 == NULL) return NULL;

    k3->setLeft(SingleLeftRotation(k3->getLeft()));

    return SingleRightRotation(k3);
}

Case 3

An insertion into left subtree of the right child of α.

Solution: Double Right Left Rotation

As the name shows, this give rotation also involves two step rotations.

1. Right Rotation

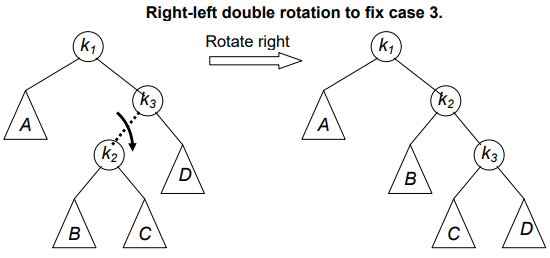
2. Left Rotation

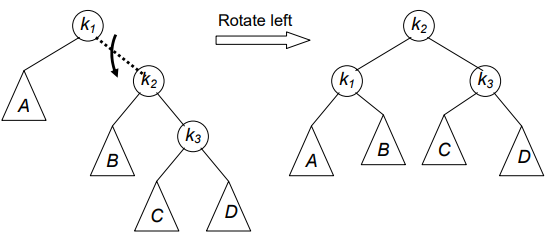
C++ code for Double Right Left Rotation

TreeNode <int> * doubleRightLeftRotation(TreeNode <int> *k1) {
    if (k1 == NULL) return NULL;

    k1->setRight(SingleRightRotation(k1->getRight()));

    return SingleLeftRotation(k1);
}

Fixing the Fig.18 of Example in Insertion of the nodes in AVL tree

It’s time to fix our unsolved problem in Fig 18 which led us to study the cases of rotation. 🙂

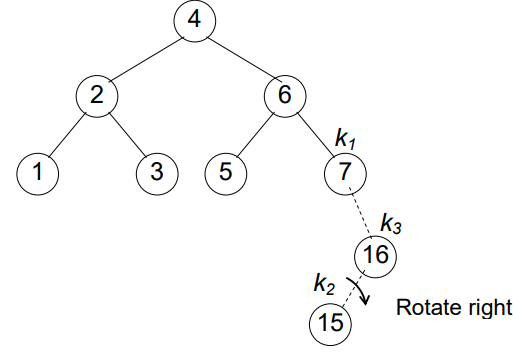
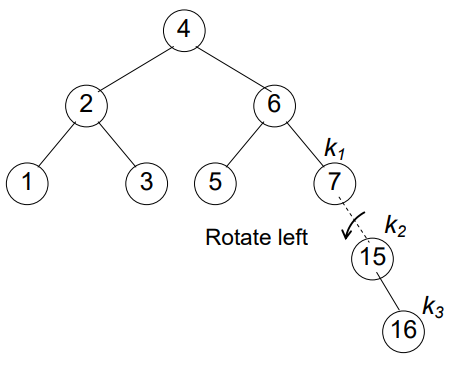
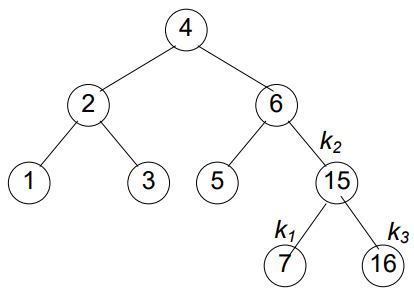
🎉Congratulation! In Fig 9, tree has become balanced. Let’s insert more.🤓

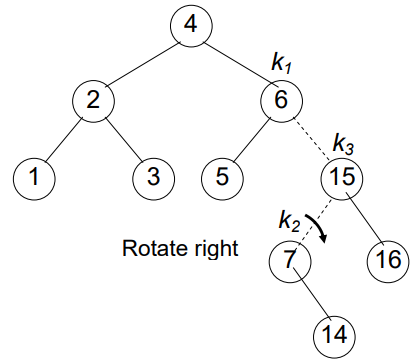
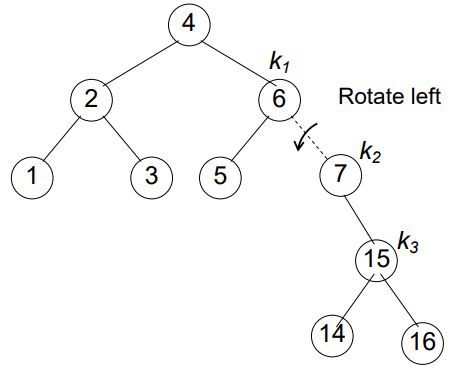
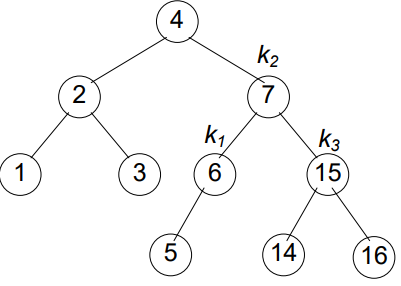
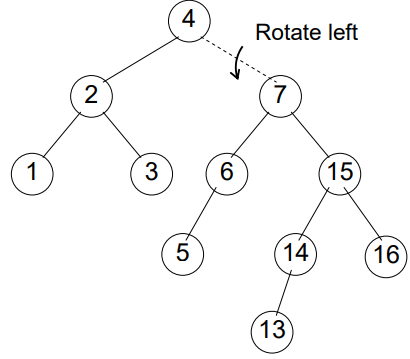
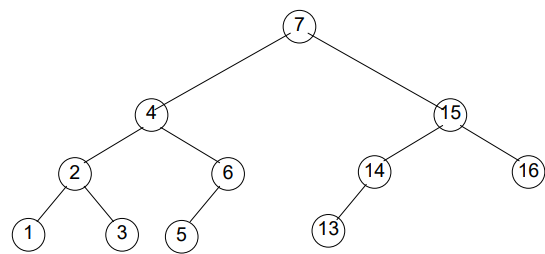
C++ code for avlInsert method

While considering our above rotation cases, we can insert nodes in AVL tree.

TreeNode<int>* avlInsert(TreeNode<int>* root, int info) {
    if( info < root->getInfo() ){
	root->setLeft(avlInsert(root->getLeft(), info));
	int htdiff = height(root->getLeft()) – height(root->getRight());
	if( htdiff == 2 )
	    if( info < root->getLeft()->getInfo() ) //outside insertion case
	        root = singleRightRotation( root );
		else // inside insertion case
		    root = doubleLeftRightRotation( root );
 }
    else if(info > root->getInfo() ) {
	root->setRight(avlInsert(root->getRight(),info));
  	    int htdiff = height(root->getRight()) – height(root->getLeft());
	if( htdiff == 2 )
	    if( info > root->getRight()->getInfo() )
		root = singleLeftRotation( root );
	    else
		root = doubleRightLeftRotation( root );
    }
    // else a node with info is already in the tree. In
    // case, reset the height of this root node.
    int ht = Max(height(root->getLeft()), height(root->getRight()));
    root->setHeight( ht + 1 ); // new height for root.
    return root;
}

REFERENCE: CS301 Handouts (page 237 to 264)