Circularly Linked List

What is circularly linked list?

“A type of singly linked list whose last node is connected with the first node.”

Let’s make it more clear, circularly linked list has node who has only next pointer pointing (same as the singly linked list), but the next field of last node is pointing to the first node. This almost makes the ring or circle of the nodes.

Why circularly linked list?

The next method in the singly-linked list or doubly-linked list moves the current pointer to the next node and every time it checks whether the next pointer is NULL or not. Similarly the back method in the double-linked list has to be employed carefully if the current is pointing the first node. In this case, the prev pointer is pointing to NULL. If we do not take care of this, the current will be pointing to NULL. So if we try to access the NULL pointer, it will result in an error. To avoid this, we can make a circularly linked list.

How circularly linked list looks like?

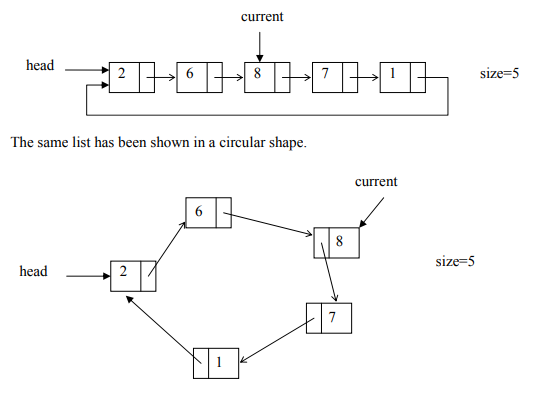
NOTE: Viewing circularly linked list like this doesn’t mean that it relies like this on memory. We already know that the nodes in linked list are distributed over different section of the memory, only pointers connect them to one another.

Use of circularly linked list

Josephus Problem

Consider there are 10 persons. They would like to choose a leader. The way they decide is that all 10 sit in a circle. They start a count with person 1 and go in clockwise direction and skip 3. Person 4 reached is eliminated. The count starts with the 5^th and the next person to go is the 4rth in count. Eventually, a single person remains which is the leader.

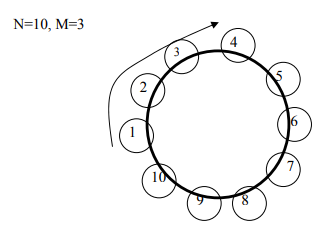
M = No. of counts

N = No. of persons

Following images show the implementation of Josephus Problem.

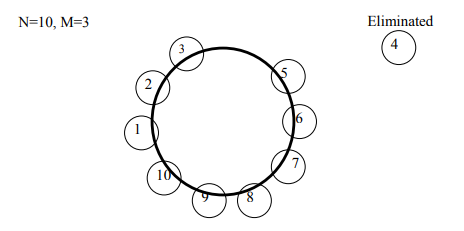
After eliminating the number 4, we’ll start our counting from number 5. Counting up to three, we’ve number 8 which is eliminated and so on.

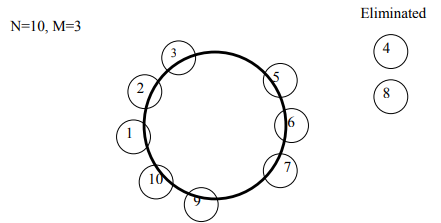
We’ll continue this procedure until only one person remains, in this case, 5 will remain intact.

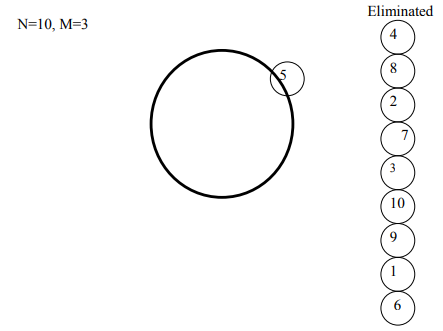
Solving Josephus Problem using C++

void main(int argc, char* argv[]) {
	CList list;
	int i, N = 10, M = 3;
	for (i=1; i<=N; i++) { list.add(i); }
	list.start();
	while (list.length() > 1) {
		for (i=1; i<=M; i++) list.next();
		cout << "remove: " << list.get() << endl;
		list.remove();
	}
	cout << "leader is: " << list.get() << endl;
}

Benefits of using Circularly Linked List

• It makes solution trivial. We’d to just write the code of some lines that solved the whole problem.
• Using array instead of circularly linked list in Josephus problem could lead to complexity. Because for array, we’d to write code to move back and forth and to remove different elements properly in a particular order.

REFERENCE: CS301 Handouts (page 40 to 48)