Deletion of Node in AVL tree

Let’s Start!

We know that insertion in a height-balanced tree requires at most one single rotation or one double rotation. But for deletion:

• We can use rotations to restore the balance when we do a deletion.
• We may have to do a rotation at every level of the tree. Thus in the worst case of deletion we have to do log N (log with base 2) rotations. As log N (log with base 2) is the number of levels of a tree of N nodes.

Delete the node as in binary search tree. Just balance the tree after deletion.

Before you start!

Know that the arrow direction inside the node is showing that this direction is heavier (have more nodes) as compared to the other side.

If the arrow is single, then the balance is 1 or -1. And if arrows are double, then the balance is 2 or -2.

And the plane bar/line is showing that the node’s balance is 0 (Number of nodes in left and right side are same).

Cases in Deletion

• Case I: The node to be deleted is the leaf node i.e. it has no right or left child. It is very simple to delete such node. We make the pointer in the parent node pointing to this node as NULL. If the memory for the node has been dynamically allocated, we will release it.
• Case II: The node to be deleted has either left child (subtree) or right child (subtree). In this case we bypass the node in such a way that we find the in-order successor of this node and then link the parent of the node to be deleted to this successor node. Thus the node was deleted.
• Case III: The node to be deleted has both the left and right children (subtree). This is the most difficult case. In this case we find the in-order successor of the node. The left most node of the right subtree will be the in-order successor of it. We put the value of that in-order successor node into the node to be deleted. After it we delete the in-order successor node recursively.

Here, we’ll discuss only five cases of deletion.

Case 1a

“The parent of the deleted node had a balance of 0 and a node was deleted in the parent’s left subtree.”

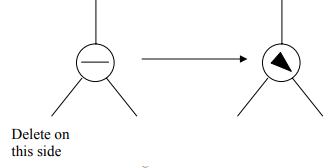
You can see, when we delete the node from left side, the arrow directs towards right side showing that right side is heavy as compared to the left side. To avoid this, follow the below action:

Action: Change the balance of the parent node and stop. No further effect on balance of any higher node.

Case 1b

“The parent of the deleted node had a balance of 0 and the node was deleted in the parent’s right subtree.”

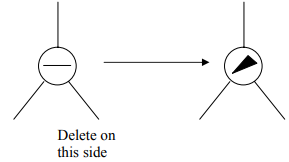
Action: Change the balance of the parent node and stop. No further effect on balance of any higher node (same as case 1a).

Case 2a

“The parent of the deleted node had a balance of 1 and the node was deleted in the parent’s left subtree.”

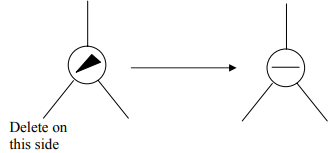
Action: Change the balance of the parent node. May have caused imbalance in higher nodes so continue up the tree.

Case 2b

“The parent of the deleted node had a balance of -1 and the node was deleted in the parent’s right subtree.”

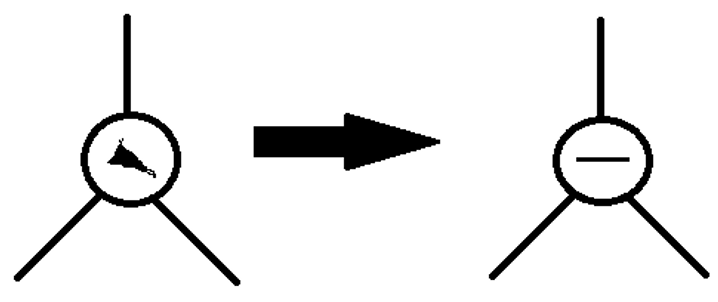
Action: Change the balance of the parent node. May have caused imbalance in higher nodes so continue up the tree.

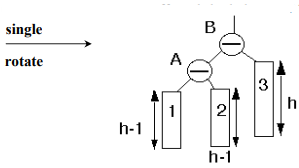
Case 3a

“The parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was balanced.”

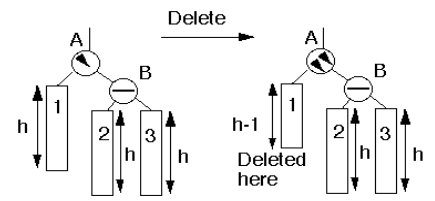
Action: Perform single rotation, adjust balance. No effect on balance of higher nodes so stop here.

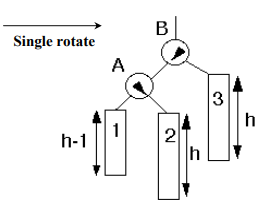
Node A has become the left subtree of node B and node 2 left subtree of node B has become the right subtree of node A. The balance of node B is tilted towards left and balance of node A is tilted towards right but somehow, both are within AVL limits. Hence, after a single rotation, the balance of the tree is restored in this case.

Case 4a

“Parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was unbalanced.”

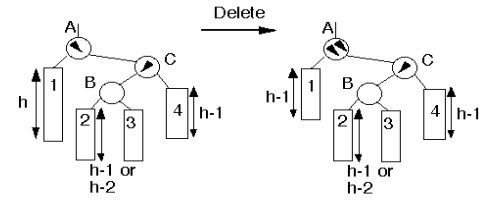
Action: Double rotation at B. May have affected the balance of higher nodes, so continue up the tree.

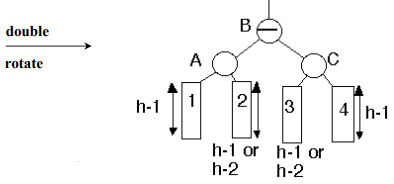
Node A, which was the root node previously, has become the left child of the new root node B. Node C, which was the right child of the root node C has now become the right child of the new root node B.

Case 5a

“The parent had balance of -1 and the node was deleted in the parent’s left subtree, right subtree was unbalanced.”

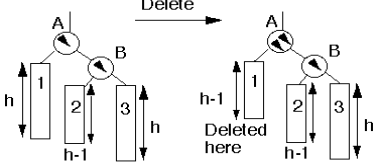
Action: Single rotation at B. May have affected the balance of higher nodes, so continue up the tree.

In the End

3b, 4b, and 5b cases also exist. Here, we discussed only 5. 🙂

If we perform deletion, the balance of tree might be get changed on higher nodes. So, we’ve to continue searching up to the tree to check the balance. We can do this using recursive calls.

REFERENCE: CS301 Handouts (page 265 to 278)