Evaluating Postfix Expression

Let’s Start

In the postfix form, parentheses are not used. Consider the infix expressions as ‘4+3*5’ and ‘(4+3)*5’. The parentheses are not needed in the first but are necessary in the second expression. The postfix forms are:

4+3*5   ->     435*+

(4+3)5    ->  43+5

Procedure of Evaluation

Each operator in a postfix expression refers to the previous two operands. As the operators are binary (i.e. *, +), so two operands are needed for each operator.

Each time we read an operand, we will push it on the stack. We are going to evaluate the postfix expression with the help of stack. After reaching an operator, we pop the two operands from the top of the stack, apply the operator and push the result back on the stack.

Algorithm in Pseudo code

Stack s; // declare a stack

while( not end of input ) { // not end of postfix expression
 	e = get next element of input
	if( e is an operand )
		s.push( e );
	else {
		op2 = s.pop();
		op1 = s.pop();
		value = result of applying operator ‘e’ to op1 and op2;
		s.push( value );
	}
}
finalresult = s.pop();

Postfix Evaluation Example

Let’s take given expression as out example to understand the evaluation process of postfix.

6 2 3 + – 3 8 2 / + * 2 ↑ 3 +

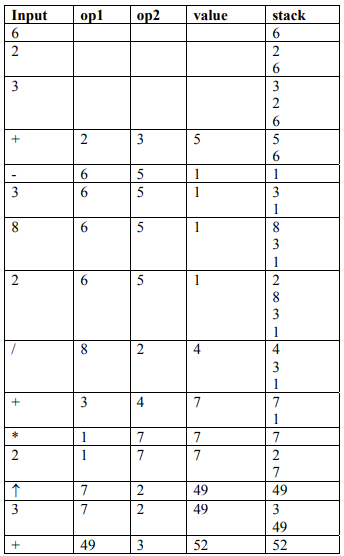
The above figure shows that the we continue pushing the operands onto the stack until we find the operator (binary in this case). So, seeing this operator, we pop top two elements/operands from the stack and perform operation on them and then again push back to the stack.

Infix to Postfix Conversion

There’re lot of scenarios when we need infix to postfix conversion. One of the most popular example is spreadsheet, where user give the expression in infix form. To evaluate it, this infix form is converted to postfix form.

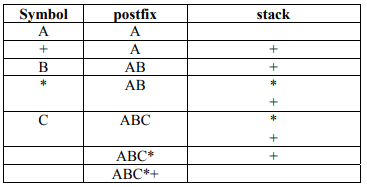
In case of ‘(A+B)*C’, the closing parenthesis indicates that ‘+’ must be performed first. After sending the A and B to postfix perform, we can perform the addition due to the presence of the parenthesis.

Sometimes, we have two operators and need to decide which to apply first like in this case ‘+’ and ‘*’. In this case, we have to see which operator has higher precedence. Assume that we have a function ‘prcd(op1,op2)’ where op1 and op2 are two operators.

The function ‘prcd(op1,op2)’ will return TRUE if op1 has precedence over op2, FALSE otherwise.

Pseudocode

Stack s;
while( not end of input ) {
	c = next input character;
	if( c is an operand )
		add c to postfix string;
	else {
		while( !s.empty() && prcd(s.top(),c) ){
		op = s.pop();
		add op to the postfix string; 
	}
	s.push( c );
}
while( !s.empty() ) {
op = s.pop();
add op to postfix string;
}

We read the input character and store it in the ‘c’. Here the input character does not mean one character, but an operand or an operator.

Take deep breath, it’s not hard! Let’s go step by step to understand the procedure:

• Continue pushing things until there is not the end of input.
• If c is the operand, send it to the postfix string.
  • The order of operands won’t change during this process, but order of operators might be changed and we’ll do evaluation depending upon the precedence of the operator through prcd(op1, op2) function.
• If c is the operator, push it to the stack.
• If c faces any operator having high precedence over previous operator, then send this previous operator to the postfix string. Otherwise just simply push it to the stack.
• In this way, we’ll get our expression, converted from infix to postfix.

Dealing Parenthesis in the Expression

Sometimes we do need the parenthesis in the infix form. We use it when we want to perform the operator of lower precedence first and higher precedence later.

When an open parenthesis ‘(‘ is read, it must be pushed on the stack. This can be done by setting prcd(op,‘(‘ ) to be FALSE. What is the reason to put the parenthesis on the stack? It is due to the fact that as long as the closing parenthesis is not found, the open parenthesis has to wait. It is not a unary or binary operator. Actually, it is a way to show or write precedence.

Also, prcd( ‘(‘,op ) is FALSE which ensures that an operator after ‘(‘ is pushed on the stack. When a ‘)’ is read. All operators up to the first ‘(‘ must be popped and placed in the postfix string. To achieve this our function prcd( op,’)’ ) should return true for all the operators.

Pseudocode

We’ll just change our s.push(c) with our following code:

if( s.empty() || symb != ‘)’ )
	s.push( c );
else
	s.pop(); // discard the ‘(‘

Functionality  in prcd function

The following functionality has to be added in the prcd function.

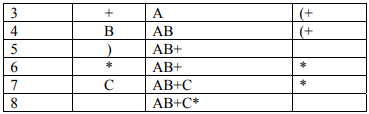
Let’s see the conversion from infix to postfix in case we use parenthesis in the infix form.

Reference: CS301 Handouts (page 63 to 72)