In-order Traversal of Threaded Binary Tree

Introduction

How will you find the next in-order successor in threaded binary tree? Answer is obvious, you’ll go continuously move to the left of each node until you don’t get the leaf node. But how will we find the leaf node in threaded binary tree whose leaf node has LTH and RTH as left and right pointers representing their in-order predecessor and successor respectively? Don’t worry, that’s what we’re going to cover in this article. Make sure you know what the Threaded Binary Tree is. 😊

Strategy of finding In-order Successor in Threaded Binary Tree

Pointer “p” is pointing to the current node.

Leaf nodes in threaded binary tree have threads (LTH, RTH) pointing to their in-order predecessor and successor. For assurance of being leaf nodes, we set their flags on.

• If the RTH flag of the p node (the node passed in the parameter) is thread then it will return the node being pointed by the right thread (p->R), which would be its in-order successor.
• Otherwise, It goes to the right node of p and starts pointing it using the same p pointer. From there it keeps on moving (in a loop fashion) towards the left of the node as long as the statement p->LTH == child is true. After this loop is terminated, the node p is returned.

We’re going to have detailed study about this. First, have a look at its C++ code to get better idea about what we were talking about. 🤓

C++ Code for In-order successor in Threaded Binary Tree

TreeNode* nextInorder(TreeNode* p) {
    if(p->RTH == thread)
        return(p->R);
    else {
        p = p->R;
        while(p->LTH == child)
        p = p->L;
        return p;
    }
}

In-order Traversal of Threaded Binary Tree through Figures

Assume, we’re at node 4, show in figure-1.

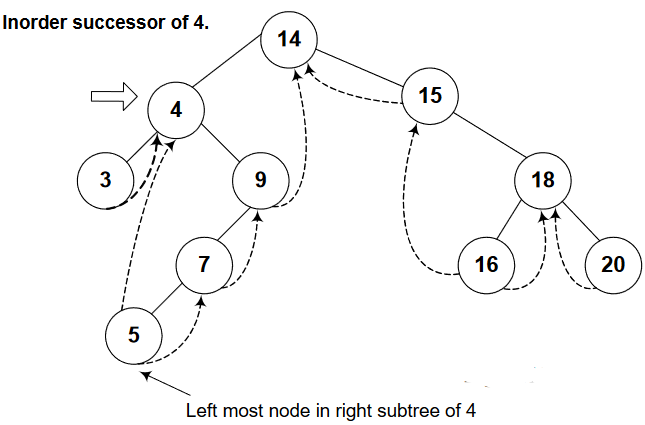
In-order successor of node 4 will be the left-most node of its right sub-tree. To reach there, we’ll go to the right of node 4 (which is node 9), then will continue our journey until the node with no child comes.

Here is the code we’re following in this:

p = p->R;
while(p->LTH == child)
p = p->L;
return p

• Take the right node.
• Continue journey if it has left child.
• Take the left node.
• Return it.

At node 5, the condition if(p->RTH == thread) will be true and node 7 will be come out through return(p->R) as in-order successor of node 5. After node 7, node 9 will be there, later, node 14.

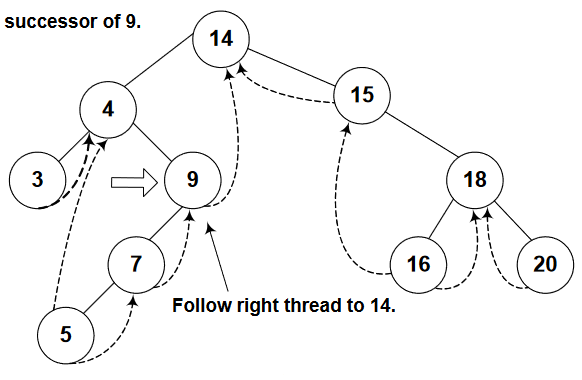
Problem in finding In-order successor of Threaded Binary Tree

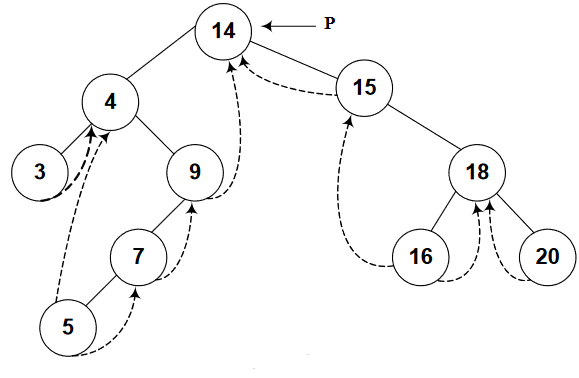
What if “p” is initially at root node (14 in our case), shown in figure-3? We stuck. 🙃 That’s how it happens:

Right thread for node 14 is not set, so our code will jump to the else part, which takes the right node of “p” (node 15 in our case). See figure-4.

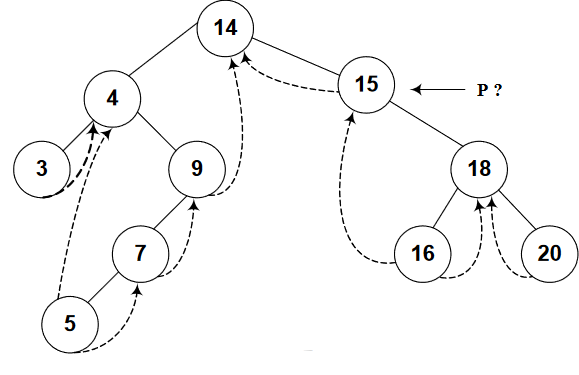
While we should go to the node 3 in case of in-order traversal, in other words, “3” should be printed first. But we’re going to the right of “14” instead of left.

Our In-order traversal prints the nodes in this way: 3, 4, 5, 6, 7, 9 …

Trick to Solve the Problem in Threaded Binary Tree

We will insert an extra node in the binary tree and call it as a dummy node.

See figure-5.

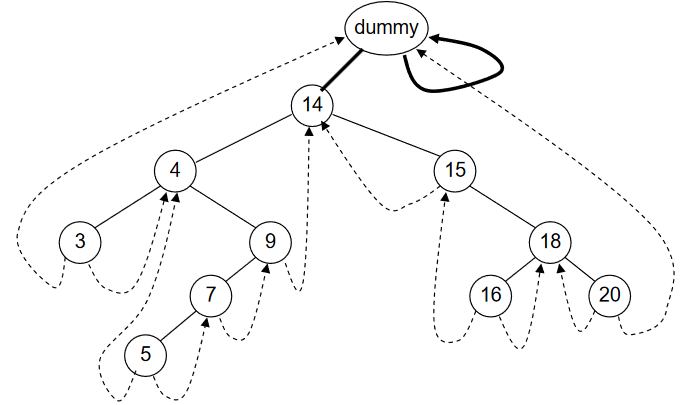
• This dummy node has either no value or some dummy value.
• The left pointer of this node is pointing to the root node of the tree while the right pointer is seen pointing itself i.e. to dummy node.
• Left thread of the left most node is pointing towards the dummy node.
• Right thread of the right most node is pointing towards the dummy node.

C++ Code

/* This routine will traverse the binary search tree */

void fastInorder(TreeNode* p) {
    while((p=nexInorder(p)) != dummy) cout << p->getInfo();
}

Conclusion

1. Check whether the right pointer of this node is not thread. If so, then it is advisable to move the pointer towards the right pointer of the node.
2. We will go to the while loop and start moving on the left of the node till the time we get a node with the left pointer as thread.
3. The pointer p will move from dummy to node 14. As the left pointer of node 14 is not thread so p will move to node 4. Again the p will move to node 3. As the left pointer of p is thread, the while loop will finish here. This value will be returned that is pointing to node 3.

This in-order traversal will be faster than the recursive in-order traversal. We’ve not used additional memory for this routine. We are using the null links and putting the values of thread in it.

In the recursive routines, we have to stop the recursion at some condition. Otherwise, it will keep on executing and lead to the aborting of our program.

REFERENCE: CS301 Handouts (page 316 to 326)