Let’s Start!
AVL tree, which is already balanced. Before we perform insertion, we need to careful about the balance of tree and the order of nodes.
Problem
Consider the following AVL tree:
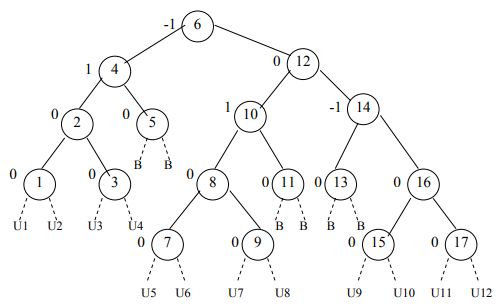
We have used two labels B and U for different positions where a node can be added. The label B indicates that if we add a node at this position, the tree will remain balanced tree. On the other hand, the addition of a node at the position labeled as U1, U2 ….U12, the tree will become unbalanced.
We may conclude that the tree becomes unbalanced only if the newly inserted node:
- Is a left descendent of a node that previously had a balance of 1 (in the Fig 1 these positions are U1, U2 …..U8).
- Or is a right descendent of a node that previously had a balance of –1 (in the tree in Fig 1 these positions are U9, U10, U11 and U12).
Now, see the following figure:
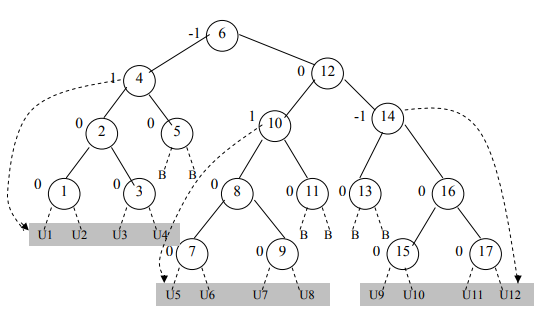
As the U1, U2, U3, U4 and U5, U6, U7, U8 are the left descendants of the node having balance of 1. And U9, U10, U11, U12 are the right descendants of the node having balance of -1. This will make the tree unbalanced.
Zooming into the Problem
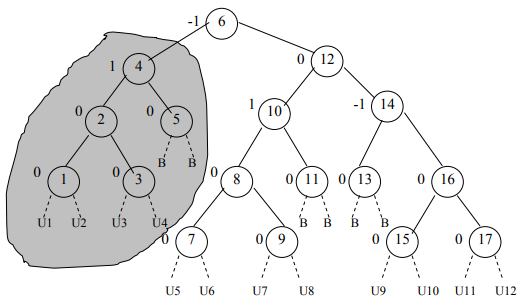
To understand the problem clearly, consider the node that has a balance 1 in the previous tree. This is the root of the left subtree of the previous tree. This tree is shown as shaded in the following figure.
Now, we’ll observe just small section of the tree. We’ve put the nodes’ balance as their value and A, B as their names. T1, T2, and T3 are representing the trees. The dotted line is showing the difference between the height/depth of left and right subtree (As of node A is 1 that’s the balance of node A) in Fig 4.
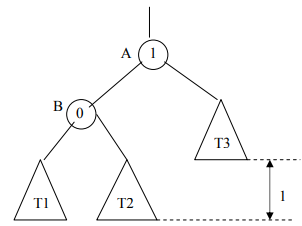
Now, let’s add the new node in T1 (left subtree of the node A having balance of 1).
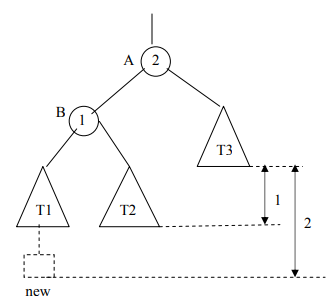
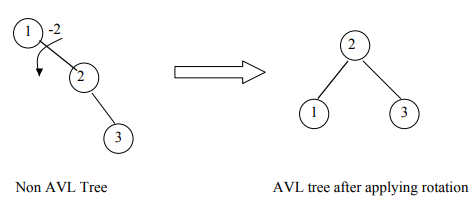
You can see in Fig 5, the balance of node A has become 2, which doesn’t make this tree an AVL tree and leads to more time in searching process of node in the tree.
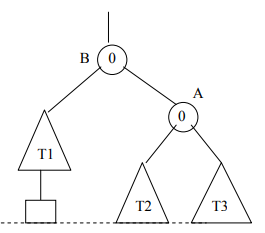
When we rearrange the tree in figure 5, as a result, we get the balanced tree in figure 6.
Example (AVL Tree Building)
Let’s insert the nodes in the AVL tree; moreover, you’ll observe that when the balance of the tree gets disturbed, we rearrange it. Afterward, we perform the next insertion.
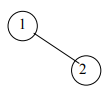
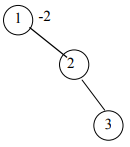
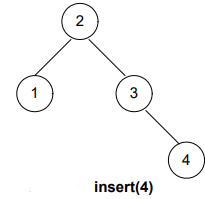
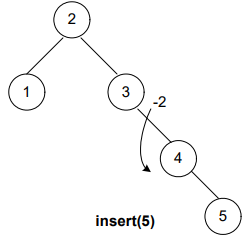
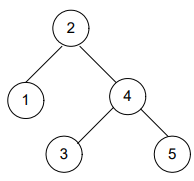
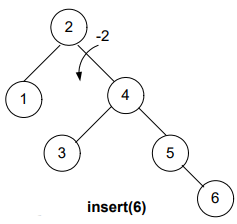
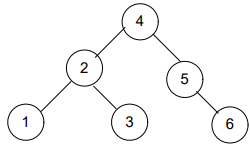
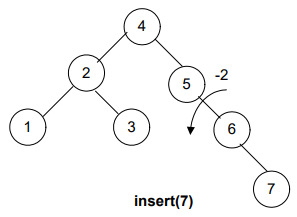
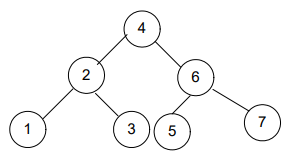
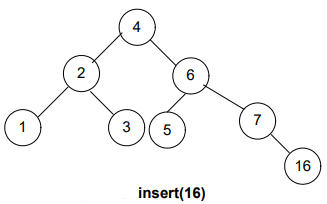
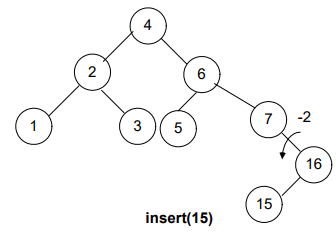
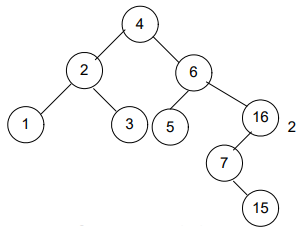
Now, what’s next? It’s still unbalanced!
We’ll discuss Cases of Rotation to overcome this problem.
REFERENCE: CS301 Handouts (page 224 to 237)








[…] know that insertion in a height-balanced tree requires at most one single rotation or one double rotation. But for […]
After insertion of node in the tree, the tree might become unbalanced. So, to make it balance, we need to do rotations. Consider the section Zooming into the problem.
[…] we know that, in Example of Insertion of nodes in AVL tree, the single rotation was not of great help to make the balance of […]
In Example, we stuck at figure 19 (last figure). When the balance at node “16” became 2. And single rotation was not helping in restoring the balance. So, to overcome this, we required some other technique which is double rotation (discussed in cases of rotation).