Level order Traversal
“In level order traversal, we visit the nodes at each level before proceeding to the next level.”
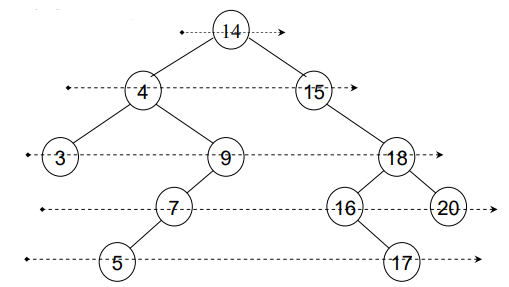
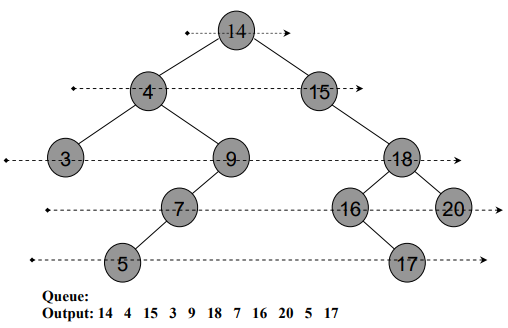
In the above figure, levels have been shown using arrows:
- At the first level, there is only one number 14.
- At second level, the numbers are 4 and 15.
- At third level, 3, 9 and 18 numbers are present.
- At fourth level the numbers are 7, 16 and 20.
- While on fifth and final level of this tree, we have numbers 5 and 17.
See the C++ code for Level-order traversal:
void levelorder( TreeNode <int> * treeNode ) {
Queue <TreeNode<int> *> q;
if( treeNode == NULL ) return;
q.enqueue(treeNode);
while( !q.empty() ) {
treeNode = q.dequeue();
cout << *(treeNode->getInfo()) << " ";
if(treeNode->getLeft() != NULL )
q.enqueue( treeNode->getLeft());
if(treeNode->getRight() != NULL )
q.enqueue( treeNode->getRight());
}
cout << endl;
}See this level order traversal in detail through following figures:
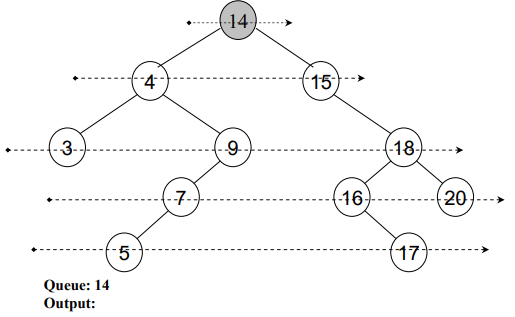
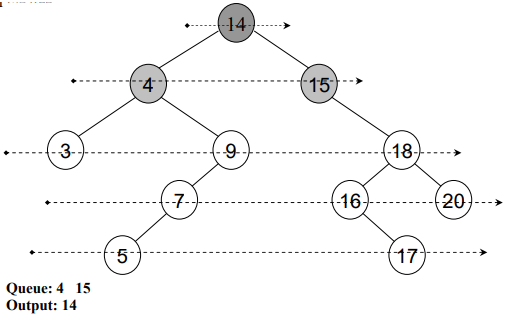
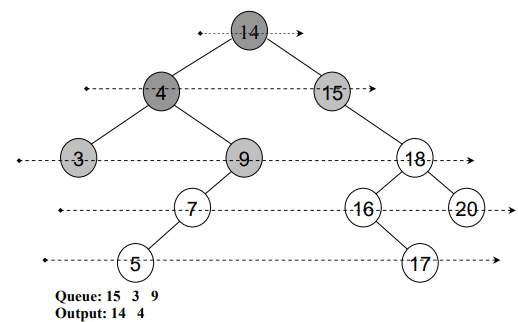
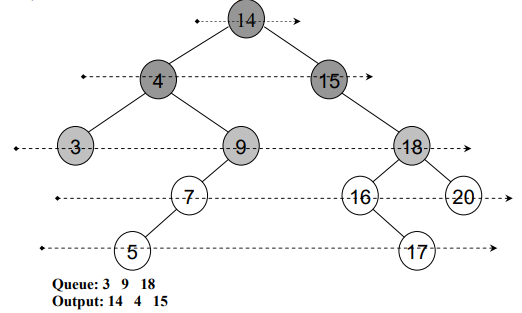
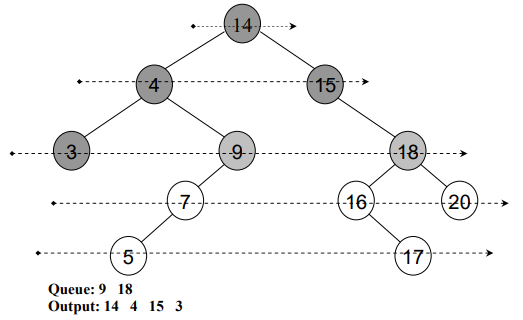
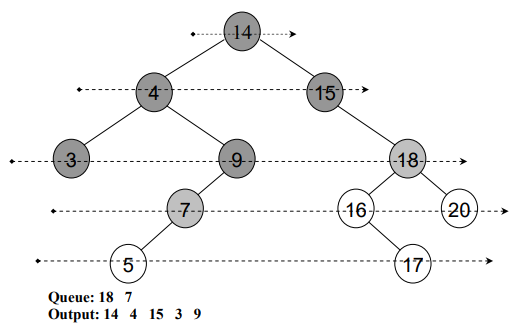
After traversing all the nodes, see Fig 8:
Deleting a Node from BST
It’s common with many data structures that the hardest operation is deletion. Once we’ve found the node to be deleted, we need to consider several possibilities.
Case 1
“If the node is a leaf, it can be deleted quite easily.”
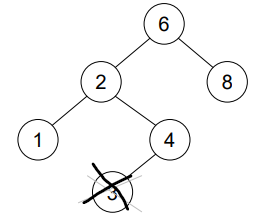
Case 2
“If the node has one child, the node can be deleted after its parent adjusts a pointer to bypass the node and connect to in-order successor.”
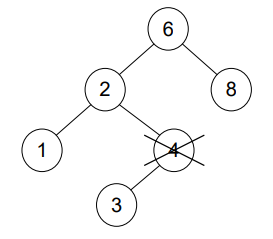
Case 3
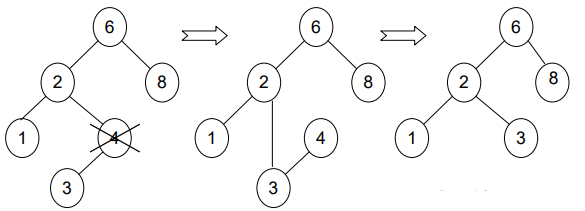
“It’s a little bit complicated, when the node to be deleted has both left and right subtrees. The strategy is to replace the data of this node containing the smallest data of the right subtree and recursively delete that node.”
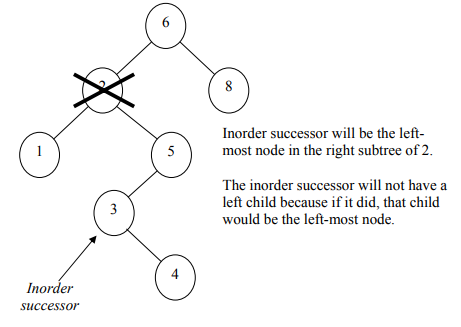
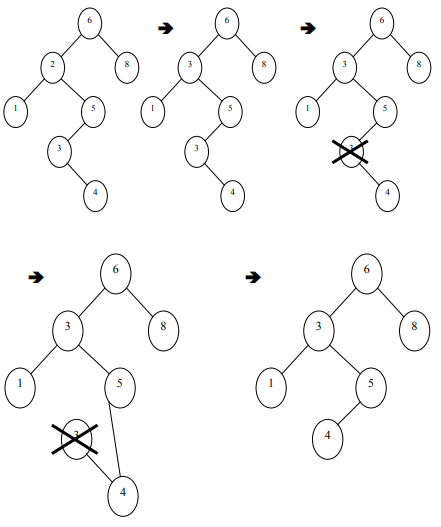
Deletion C++ code
Have a look at the C++ code of deletion:
/* This method is used to remove a node from the BST */
TreeNode<int>* remove(TreeNode<int>* tree, int info) {
TreeNode<int>* t;
int cmp = info - *(tree->getInfo());
if( cmp < 0 ){ // node to delete is in left subtree
t = remove(tree->getLeft(), info);
tree->setLeft( t );
}
else if( cmp > 0 ){ // node to delete is in right subtree
t = remove(tree->getRight(), info);
tree->setRight( t );
}
//two children, replace with inorder successor
else if(tree->getLeft() != NULL && tree->getRight() != NULL ){
TreeNode<int>* minNode;
MinNode = findMin(tree->getRight());
tree->setInfo( minNode->getInfo() );
t = remove(tree->getRight(), *(minNode->getInfo()));
tree->setRight( t );
}
else { // case 1
TreeNode<int>* nodeToDelete = tree;
if( tree->getLeft() == NULL ) //will handle 0 children
tree = tree->getRight();
else if( tree->getRight() == NULL )
tree = tree->getLeft();
else tree = NULL;
delete nodeToDelete; // release the memory
}
return tree;
}REFERENCE: CS301 Handouts (page 158 to 172)







