Operations on Binary Tree

Let’s Start!

Applications of Binary Tree

The binary tree serves as a useful structure for making two-way decisions at each point.

It helps in fast search of element from the list. Although, linked list contributed in this regard. But linked list requires more searches as compared to the Binary Tree.

Searching for Duplicates

Let’s consider following data in out example: 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5.

First Method

One way to achieve this duplication detection is that we compare each element with elements preceding it.

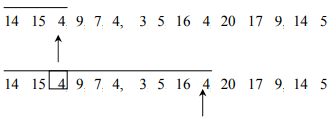
This procedure involves a large number of comparisons, if the list of numbers is large and is growing. A linked list can handle the growth but the number of comparisons may still be large.

Second Method

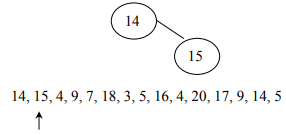
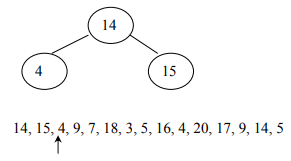
The construction of the binary tree follows a unique method. A node creates the first number in the list, then assigns it as the root of the binary tree. Initially, both left and right sub-trees of the root are empty. We take the next number and compare it with the number placed in the root. If it is the same, this means the presence of a duplicate. Otherwise, we create a new tree node and put the new number in it. If the second number is less than the one in the root, turn the new node into the left child of the root node. If the number is greater than the one in the root, turn the new node into the right child.

The smaller node goes to the left of root while greater node goes to the right of the root

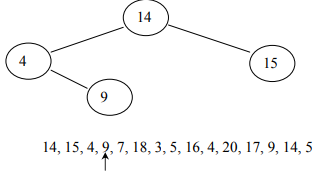
After adding the rest of all elements:

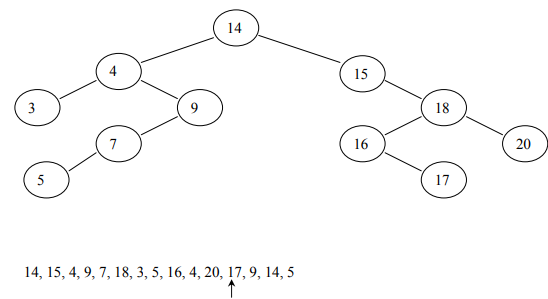
Trace of Insert

To insert an element in the binary tree, we need to set up the tracking system. To understand this, see the below code:

void insert (TreeNode <int> * root, int * info) {
	TreeNode <int> * node = new TreeNode <int> (info);
	TreeNode <int> * p, * q;
	p = q = root;
	while( *info != *(p->getInfo()) && q != NULL ) {
		p = q;
		if( *info < *(p->getInfo()) )
			q = p->getLeft();
		else
			q = p->getRight();
	}

	if( *info == *( p->getInfo() ) ) {
		cout << "attempt to insert duplicate: " << *info << endl;
		delete node;
	}
	else if( *info < *(p->getInfo()) )
		p->setLeft( node );
	else
		p->setRight( node );
} // end of insert

To understand this above code, see the following images:

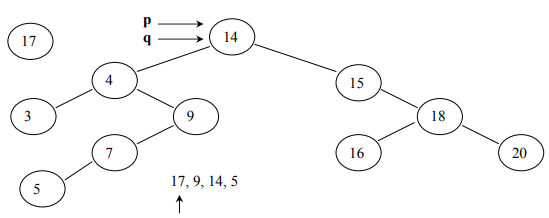
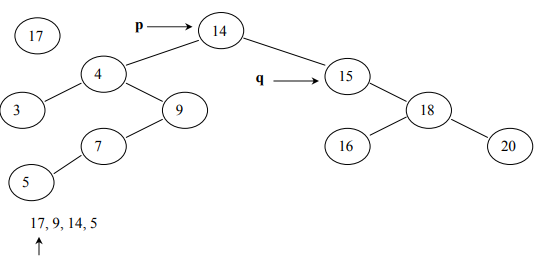
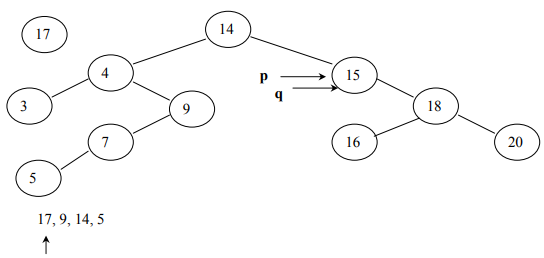
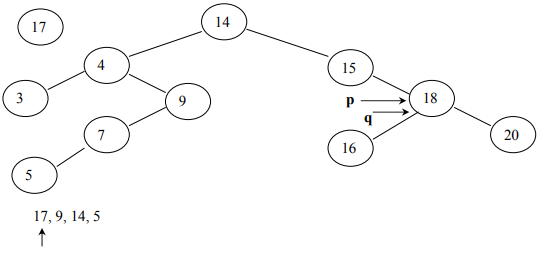
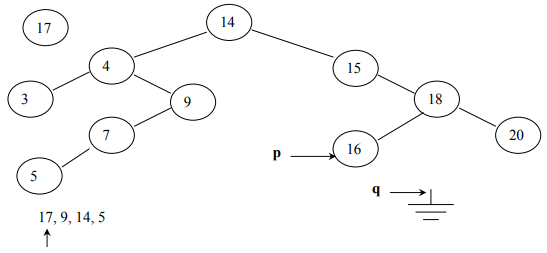
In Fig 13, (q is pointing to NULL) is the condition that causes the while loop in
the code above to terminate.

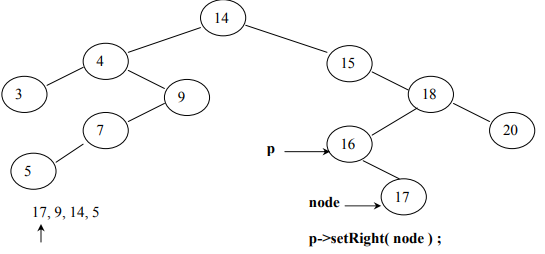
Now, our final tree will be the following:

Cost of Search

As we know that the depth of the tree can be found by the following equation:

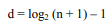
Suppose we have a complete binary tree in which there are 100,000 nodes, then its depth d will be calculated in the following fashion.

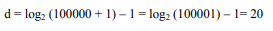
The statement shows that if there are 100,000 unique numbers (nodes) stored in a complete binary tree, the tree will have 20 levels. Now if we want to find a number x in this tree (in other words, the number is not in the tree), we have to make maximum 20 comparisons i.e. one comparison at each level. Now we can understand the benefit of tree as compared to the linked list. If we have a linked list of 100,000 numbers, then there may be 100,000 comparisons (supposing the number is not there) to find a number x in the list.

Binary Search Tree (BST)

A binary tree with such a property that items in the left sub-tree are smaller than the root and items in the right sub-tree are larger than the root is called a binary search tree (BST)

REFERNCE: CS301 Handouts (page 123 to 137)