Stack using Linked List

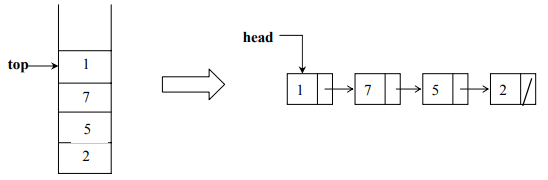
We can avoid the size limitation of a stack implemented with an array, with the help of a linked list to hold the stack elements.

Where will be push and pop in List?

For a singly-linked list, insert at start or end takes constant time using the head and current pointers respectively. As far as insertion is concerned, it is workable and equally efficient at the start and end.
Removing an element at the start is constant time but removal at the end requires traversing the list to the node one before the last. So removing from the start is better approach rather than from the end.

Fig 1: Stack using array (Left) & Stack using Linked List (Right)

Methods

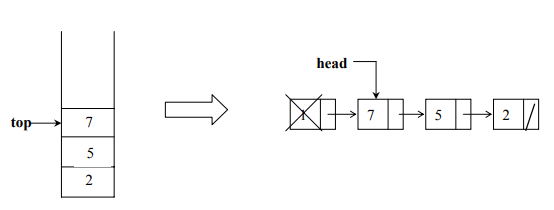
Let’s call the pop method:

int pop() {
	int x = head->get();
	Node * p = head;
	head = head->getNext();
	delete p;
	return x;
}

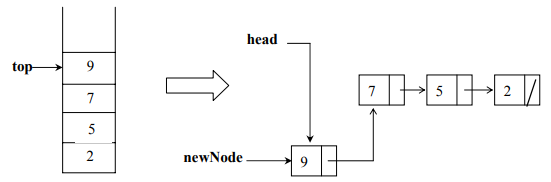
Fig 2: A node removed from the stack after the pop() call

Now, let’s call push(9):

void push(int x) {
	Node* newNode = new Node();
	newNode->set(x);
	newNode->setNext(head);
	head = newNode;
}

Fig 3: A node added to the stack after the push(9) call

See top() and isEmpty() methods

int top() {
	return head->get();
}
int isEmpty() {
	return (head == NULL);
}

Stack Implementation: Array or Linked List

Both implementations support stack operations in constant time, we will see that what are the possible reasons to prefer one implementation to the other.

Allocating and de-allocating memory for list nodes does take more time than pre-allocated array. Memory allocation and de-allocation has cost in terms of time.
List uses as much memory as required by the nodes. In contrast, array requires allocation ahead of time (Means, we fix a place for array in memory).
List pointers (head, next) require extra memory. While there is no such situation in array.
Array has an upper limit whereas list is limited by dynamic memory allocation. In other words, the linked list is only limited by the address space of the machine.

Use of Stack

Examples of uses of stack include- traversing and evaluating prefix, infix and postfix expressions.

Consider the expression A+B: we think of applying the operator “+” to the operands A and B. Firstly, + operator requires two operators or in other words “+” is a binary operator.

There are two other ways of writing expressions:

We could write +AB, the operator is written before the operands A and B. These kinds of expressions are called Prefix Expressions.
We can also write it as AB+, the operator is written after the operands A and B. This expression is called Postfix expression.

The prefixes pre and post refer to the position of the operator with respect to the two operands.

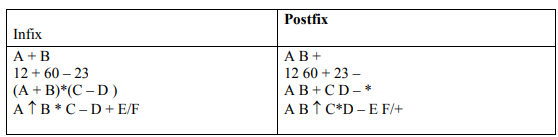
See below figure: