Threaded Binary Tree

Introduction

In many applications, binary tree traversal are carried out repeatedly. For the traversal, we perform recursion or non-recursion, but in both cases, stack is used. The excessive calls in stack can cause overhead and this can be costly. So, in the article, we’re going to discuss its solution which will help to speed-up the in-order traversal of binary tree and this method will be stack free.

Why Threaded Binary Tree?

We’ve discussed four traversal methods: In-order, pre-order, post-order, and level-order. We implemented all these traversals using recursion. Due to lot of recursive operations, the stack size keeps on growing. As a result, the performance is affected. To overcome this performance bottleneck, we can use non-recursive method but stack-driven traversal will again be an issue. The push and pop operations of stack for insertion and retrieval will again take time.

Threaded Binary Tree as a Solution

“It would be useful to modify the tree data structure which represents the binary tree so as to speed up, say, the in-order traversal process: make it stack-free.”

• Oddly, most of the pointer fields in our representation of binary trees are NULL!
• Since every node (except the root) is pointed to, there are only N-1 non-NULL pointers out of a possible 2N (for an N node tree), so that N+1 pointers are NULL.

Idea of Threaded Binary Tree

“The threaded tree data structure will replace these NULL pointers with pointers to the in-order successor (predecessor) of a node as appropriate.”

The NULL pointers are replaced by the in-order successor or predecessor. That means while visiting a node, we can tell which nodes will be printed before and after that node.

Problem

“We’ll need to know whenever formerly NULL pointers have been replaced by non NULL pointers to successor/predecessor nodes, since otherwise there’s no way to distinguish those pointers from the customary pointers to children.”

Solution of the Problem

In order to identify that the pointers has been modified to point to their in-order successor and predecessor, two flags will be required in the node. One flag will be used for successor and other for predecessor. If both the pointers were NULL, left pointer variable will be used to point in-order predecessor, the flag for this will be turned on and the right pointer variable will be used to keep in-order successor and the flag will be turned on once the successor address is assigned.

Adding Threads during Insert

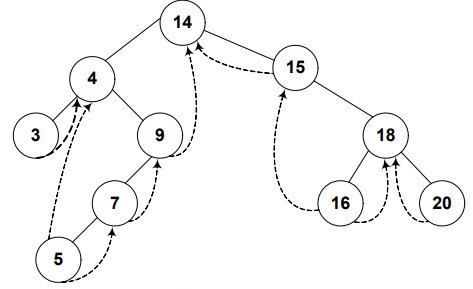
The in-order traversal of the following tree: 14, 15, 18, 20

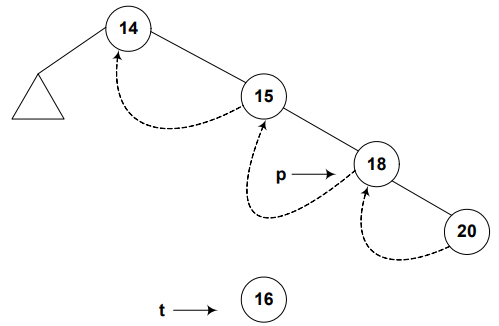
• Node 14
  • Right pointer of node 14 is pointing to node 15 (in-order successor of node 14).
  • Left pointer of node 14 is pointing to a subtree.
• Node 15
  • Right pointer of node 15 is pointing to node 18 (in-order successor of node 15).
  • Left pointer of node 15 is NULL, but we’ve indicated it with a rounded dotted line towards 14. This indicates that the left pointer points to the predecessor of the node.
• Same is for node 18 and 20 as of node 15.

Pointer t will point to the new node. Pointer p will point to the in-order successor of new node.

Finally Insertion of the Node in Threaded Binary Tree

Let’s add the node 16.

• Left and right pointers of the node 16 are NULL.
• Node 16 will be in-order predecessor of node 18 and successor of node 15.

C++ code for Node Insertion in Threaded Binary Tree

t->L = p->L; // copy the thread
t->LTH = thread;
t->R = p; // *p is successor of *t
t->RTH = thread; p->L = t; // attach the new leaf
p->LTH = child;

Be calm 🙂, we’re going to discuss this code in detail. Just have a coffee break. ☕

Step 1

Predecessor of node 18 will be the predecessor of node 16. So point the left pointer of node 16 to the predecessor of node 18.

t->L = p->L;

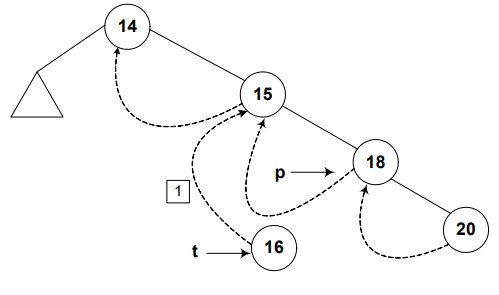
Step 2

In the next line of code, the left flag is assigned a variable thread that is used to indicate that it is on.

t->LTH = thread;

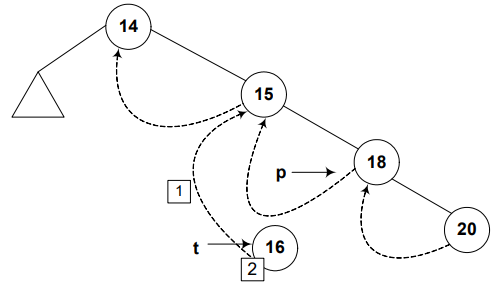
Step 3

Node 18 will be the successor of node 16, So point the right pointer of node 16 towards node 18.

t->R = p;

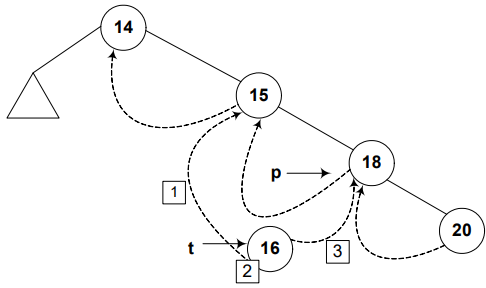
Step 4

Turn on the flag of right thread.

t->RTH = thread;

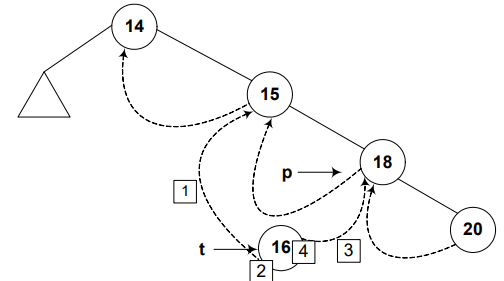
Step 5

Attach the node 16 as the left child of node 18.

p->L = t;

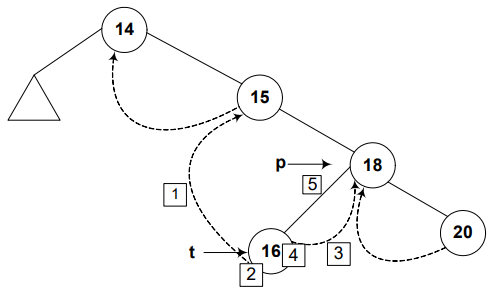
Step 6

Turn on the flag.

p->LTH = child;

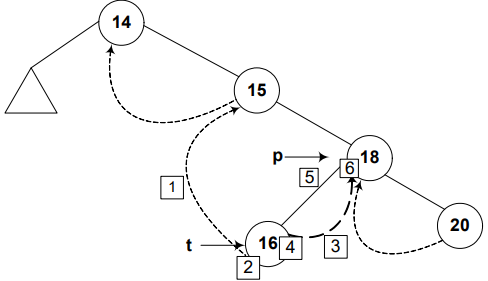
After insertion of few more node, our threaded binary tree will look like this:

Conclusion

The threaded binary tree‘s traversal speed has been improved. We replaced the NULL pointers at the leaf nodes with threads.

Left thread (LTH) points to the in-order predecessor. Right thread (RTH) points to the in-order successor.

Consider, you’re on the node 5, to find its in-order predecessor, you’ll directly use LTH to reach out instead of passing node 7, 9, and then meeting with node 4. This all goes by observing that the node’s LTH or RTH’s flag is on or off. Don’t worry, if you don’t understand this, we’re going to discuss this statement in the in-order traversal of Threaded binary tree.

REFERENCE: CS301 Handouts (page 308 to 315)