Traversing a Binary Tree

Let’s Start!

This article is going to make you learn the ways to print the elements present in BST.

Consider the following tree having three nodes: 14 is root, 4 is left sub tree, and 15 is right sub tree.

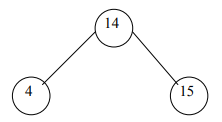
If we take permutation of the given nodes in Fig 1, then there are 6 possibilities to write theses nodes:

1: (4, 14, 15)

2: (14, 4, 15)

3: (15, 4, 14)

4: (4, 15, 14)

5: (14, 15, 4)

6: (15, 14, 4)

Let’s see the general procedure of traversing a binary tree. We know by definition that a binary tree consists of three sets i.e. root, left subtree and right subtree. The following figure depicts a general binary tree.

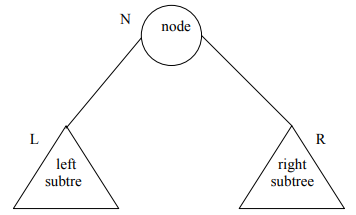
So, N = root node, L = Left subtree, R = Right subtree

Now, we’ll represent the possibilities in the following way:

1: (L, N, R)

2: (N, L, R)

3: (R, L, N)

4: (L, R, N)

5: (N, R, L)

6: (R, N, L)

Before you move ahead!

C++ Code

Pre-order Method

Pre-order traversal = (N, L, R)

void preorder(TreeNode<int>* treeNode) {
	if( treeNode != NULL ) {
		cout << *(treeNode->getInfo())<<" ";
		preorder(treeNode->getLeft());
		preorder(treeNode->getRight());
	}
}

In-order Method

In-order traversal = (L, N, R)

void inorder(TreeNode<int>* treeNode) {
	if( treeNode != NULL ) {
		inorder(treeNode->getLeft());
		cout << *(treeNode->getInfo())<<" ";
		inorder(treeNode->getRight());
	}
}

Post-order Method

Post-order traversal = (L, R, N)

void postorder(TreeNode<int>* treeNode) {
	if( treeNode != NULL ) {
		postorder(treeNode->getLeft());
		postorder(treeNode->getRight());
		cout << *(treeNode->getInfo())<<" ";
	}
}

Example

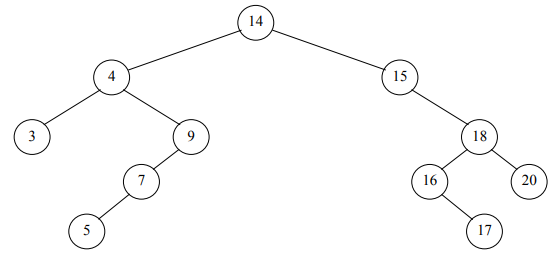
In-order traversal = 3 4 5 7 9 14 15 16 17 18 20

Pre-order traversal = 14 4 3 9 7 5 15 18 16 17 20

Post-order traversal = 3 5 7 9 4 17 16 20 18 15 14

Recursion in Traversal

Now let’s see how recursion is carried out. We know that the function calls are implemented through stacks at run time. Let’s see what happens when there is a recursive call. In a recursive call that means calling a function itself makes no difference as far as the call stack is concerned. It is the same as a function F calls a function G, only with the difference that now function F is calling to function F instead of G. The following figure shows the stack layout when function F calls function F recursively.

Aaaah! Blur image😑, but it’s visible a little bit 🤓

When F is called first time, the parameters, local variables and its return address are put in a stack, as some function has called it. Now when F calls F, the stack will increase the parameters, local variables and return address of F comes in the stack again. It is the second call to F. After coming back from this second call, we go to the state of first call of F. The stack becomes as it was at first call.

Practice Example

“Practice makes a person perfect.” 😊

Please find out the pre-order, in-order and post-order traversal of the tree given below:

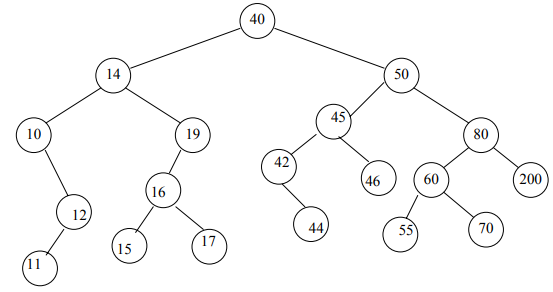
Solution

Pre-order = 40, 14, 10, 12, 11, 19, 16, 15, 17, 50, 45, 42, 44, 46, 80, 60, 55, 70, 200

In-order = 10, 11, 12, 14, 15, 16, 17, 19, 40, 42, 44, 45, 46, 50, 55, 60, 70, 80, 200

Post-order = 11, 12, 10, 15, 17, 16, 19, 14, 44, 42, 46, 45, 55, 70, 60, 200, 80, 50, 40

Bravo! 😎 You got the same solution. 🤩

REFERENCE: CS301 Handouts (page 137 to 145)