Union-by-size/weight and Union-by-height Methods for Disjoint Set ADT

Introduction

We know that when the height of tree increases, efficiency decreases especially in terms of find() operation. Union operation results in the increase of height. So, we’ve to modify the union operation to make our algorithm efficient. For this reason, we’ll discuss union by size (also called union by weight) and union by height methods. So our goal of studying these two methods is:

Modify union to ensure that heights stay small.

Union-by-Size/Weight Method

In this, we keep find operation same and just modify the union operation.

Following are the main points for this operation:

• Maintain sizes (number of nodes) of all trees, and during union.
• Make smaller tree, the subtree of the larger one.
• Implementation: for each root node i, instead of setting parent[i] to -1, set it to -k if tree rooted at “i” has k nodes.
• This is also called union-by-weight.

Find operation remains same:

// find(i):
// traverse to the root (-1)
for(j=i; parent[j] >= 0; j=parent[j])
 ;
return j;

The node can be identified as the root being the negative number and the magnitude (the absolute value) of the number will be the size (the number of nodes) of the tree. We can put the number of nodes in a tree in the root node in the negative form. It means that if a tree consists of six nodes, its root node will be containing –6 in its parent.

When the two trees would be combined for union operation, the tree with smaller size will become part of the larger one. This will cause the reduction in tree size. That is why it is called union-by-size or union-by-weight.

Pseudo Code for union-by-size/weight

Union operation after modification:

//union(i,j):
root1 = find(i);
root2 = find(j);
if (root1 != root2)
    if (parent[root1] <= parent[root2]) {
        // first tree has more nodes
        parent[root1] += parent[root2];
        parent[root2] = root1;
    }
    else {
        // second tree has more nodes
        parent[root2] += parent[root1];
        parent[root1] = root2;
    }

Let’s practice this approach.

Filling the array with “-1” showing that it’s root:

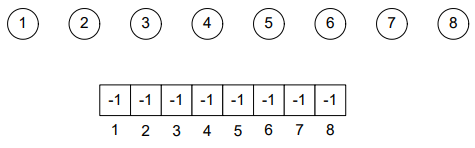
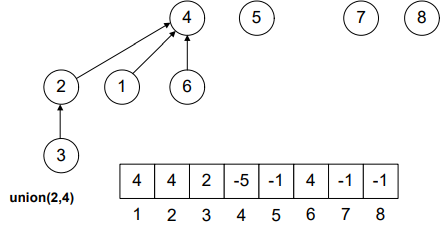
After performing union(4, 6):

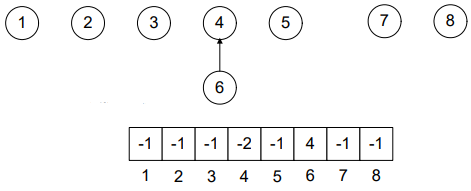
See Figure-2. The node 6 has come down to node 4. The position 6 is set to 4 indicating that the parent of 6 is 4. Moreover, the position 4 is set to “-2”, 2 showing the total number of nodes in the tree (4 and 6) and negative sign (-) along it, is showing that it’s root. While, rest of the nodes remain as it is.

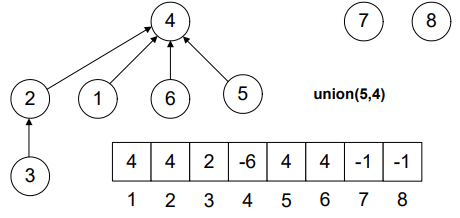
This technique continues for the next union operations.

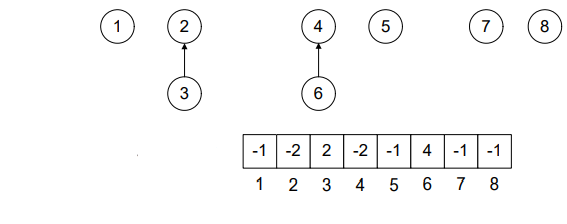
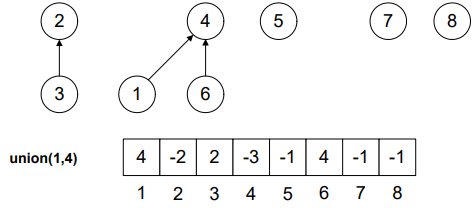
Look Figure-4. 1 was a single node tree (-1 in the array at position 1) and 4 was the root node of the tree with two elements (-2 in the array at position 4) 4 and 6. As the tree with root 4 is greater, therefore, node 1 will become part of it.

Keep in mind! The benefit of reducing the tree height is to increase performance while finding the elements inside the tree.

Analysis of Union-by-size/weight Method

Proof

• Initially, every element is at depth zero.
• When its depth increases as a result of a union operation (it’s in the smaller tree), it is placed in a tree that becomes at least twice as large as before (union of two equal size trees).

How often can each union be carried out?

Union-by-Height Method

In this, we modify find operation. We reduce the path from the node to root and make find method efficient.

Following are main points for this operation:

• Alternative to union-by-size strategy: maintain heights,
• During union, make a tree with smaller height a subtree of the other.

In this technique, we maintain the heights of the trees. It’s quite similar with the union-by-size. You can implement disjoint set ADT using any of these solutions. Both techniques i.e. union-by-size and union-by-height are equivalent and will work fine.

Sprucing up Find

We’ll optimize the find operation by using path compression (or compaction).

• During find(i), as we traverse the path from i to root, update parent entries for all these nodes to the root.
• This reduces the heights of all these nodes.

Find operation after modification:

find (i)
{
    if (parent[i] < 0)
        return i;
    else
        return parent[i] = find(parent[i]); 
}

This implementation is of recursive nature. parent[i] negative means that we have reached the root node. Therefore, we are returning i. If this is not the root node, then find method is being called recursively.

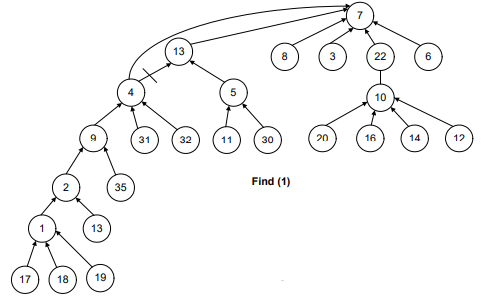
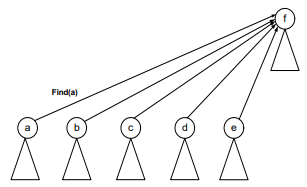
See Figure-7, the recursive call will start from find(1).

• The parent (find(1)) will return 2.
• The recursive call for 2 will take the control to node 9.
• Then to 4, 13 and then eventually to 7.
• When find(7) is called, we get the negative number and reach the recursion stopping condition.

Find(13) returns 7. Find(4) returns 7 because find(parent(4)) returns 7. That is why the link between 4 and 13 has been dropped and a new link is established between 4 and 7.

The idea is to make the traversal path shorter from a node to the root.

Now, have a look at the following figures. Whenever a path between the node and root establishes, the connection between two consecutive nodes breaks.

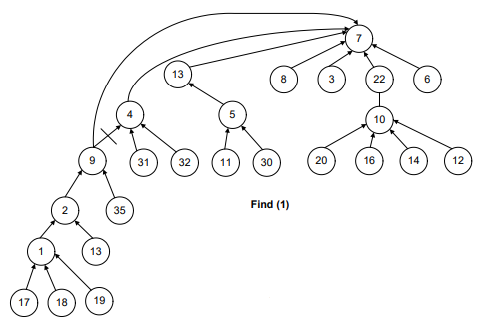
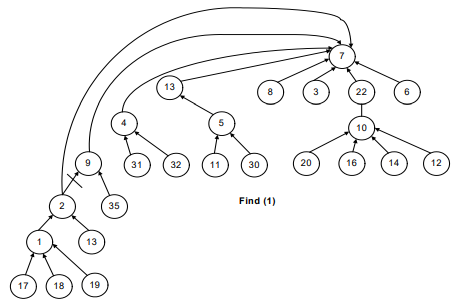
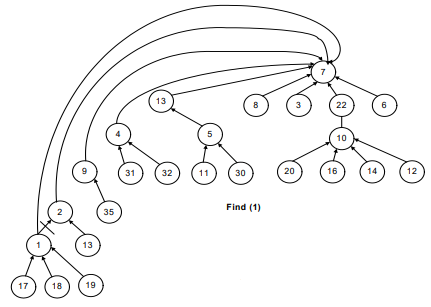
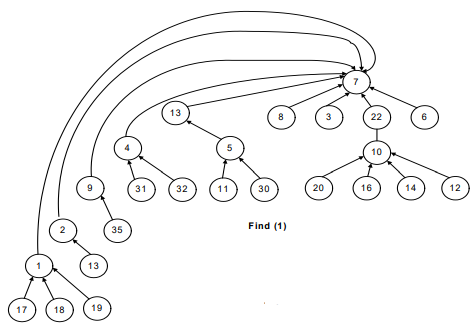
In short, we can say that this is what happens in the following images before and after the union-by-height operation.

Before union-by-height method:

After union-by-height method:

Timing with Optimization

• Theorem: A sequence of m union and find operations, n of which are find operations, can be performed on a disjoint-set forest with union by rank (weight or height) and path compression in worst case time proportional to (mÑ (n)).
• Ñ(n) is the inverse Ackermann’s function which grows extremely slowly. For all practical purposes, Ñ(n) R 4.
• Union-find is essentially proportional to m for a sequence of m operations, linear in m.

Conclusion

We used union and find methods previously, but they were not efficient due to increase in the height after union. And it was making Find operation exhaused and time consuming. To counter this problem, we discussed union-by-size/weight and union-by-height methods in this article to make our algorithm fast.

REFERENCE: CS301 Handouts (page 404 to 415)