Introduction
We’ll see that how a heap can be built and in which peculiar conditions, it should be built. Let’s say we have a large unsorted list of names and want to sort it. This list can be sorted with the help of the heap sort algorithm. We’ll build the min-heap showing the smallest integer or name having smallest alphabet as the root. After the construction of the min-heap from all the names in the list, we start taking the elements out (deleting) from the heap in order to retrieve the sorted data. In this way, the size of the heap will be decreased by one and the next name/element will be at the root position. The continuation of the process of taking out the elements from the heap will ultimately lead to a situation when there is no more node left in the tree.
Facts about Building a Heap

Use of Heap
Heap (min-heap/max-heap) can be used as database keys, used to identify information uniquely. Using the example of telephone directory that contains person’s name, address, and telephone number.
Heap is used in both priority queue and sorting.
Let’s Start
Our intention is to lower the number of searches taken by NlogN (log with base 2), for this, we’ve to this in linear time. We’ll perform our task on the binary tree given in figure-2.
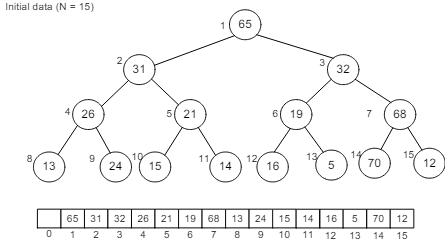
- The general algorithm is to place the N keys in an array and consider it to be an unordered binary tree.
- The following algorithm will build a heap out of N keys. for( i = N/2; i > 0; i– ) { percolateDown(i);}
Here, percolate down/up means that something is going downward or upward.
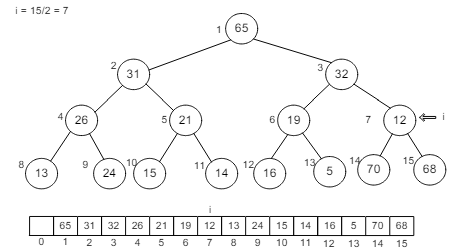
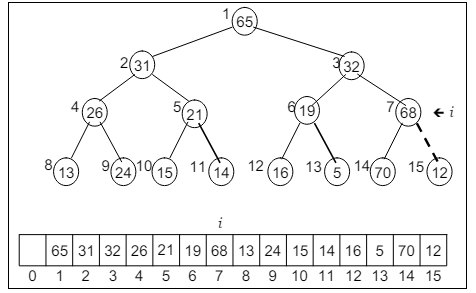
In case of decrementing: i–, ‘i’ will point to the position 6, see figure-4
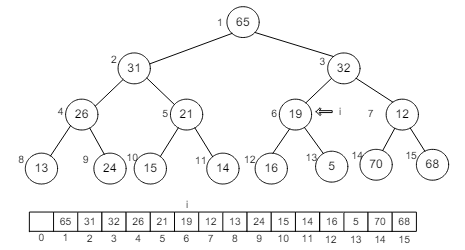
If you carefully observe the loop, and match its result with the position of ‘i’, then we get these following figures:
Children of a node at position ‘i’: Left child = 2i, Right child = 2i+1
Parent of a node at position ‘i’: i/2
We kept 0th position of the heap, empty intentionally, to apply the 2i, 2i+1 scheme. We will take this array as a complete binary tree.
Building a Min-heap
Now, our mission is to make a min-heap, because we can’t expect from the user to enter the elements in order, they might be un-ordered.
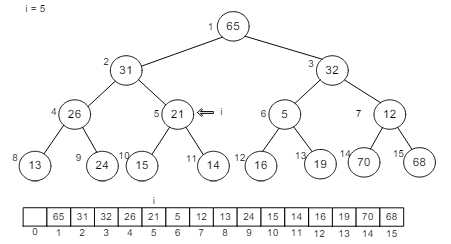
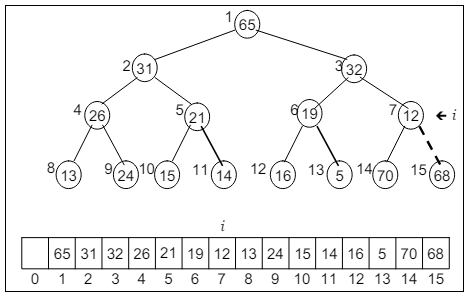
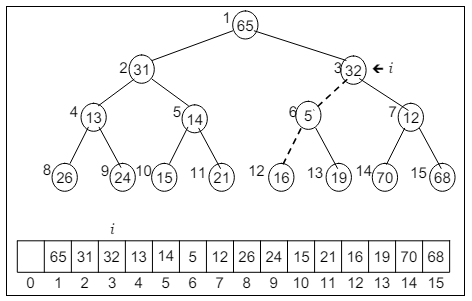
See the position of ‘i’. Every time, we’ll observe the small section of the heap, and then arrange it into min-tree. If the child is smaller, it’ll be replaced with the root. So the process continues until the whole binary tree don’t get arrange for min-heap.
Understand this using following figures:
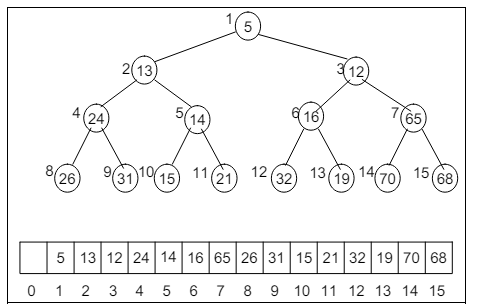
Finally we get our min-heap, shown in figure-9:
buildHeap Code
template <class eType>
void Heap<eType>::buildHeap(eType* anArray, int n )
{
for(int i = 1; i <= n; i++)
array[i] = anArray[i-1];
currentSize = n;
for( int i = currentSize / 2; i > 0; i-- )
percolateDown( i );
}PercolateDown Method
Percolate down method Interchange the node with the larger of its two children.
C++ code for this is given below:
// hole is the index at which the percolate begins.
template <class eType>
void Heap<eType>::percolateDown( int hole ){
int child;
eType tmp = array[ hole ];
for( ; hole * 2 <= currentSize; hole = child ){
child = hole * 2;
if( child != currentSize && array[child+1] < array[ child ] )
child++; // right child is smaller
if( array[ child ] < tmp )
array[ hole ] = array[ child ];
else break;
}
array[ hole ] = tmp;
}
buildHeap in Linear Time
We’ll prove mathematically that this process works better than NlogN (log with base 2).
Theorem
For a perfect binary tree of height h containing (2^h) -1 nodes, the sum of the heights of nodes is 2^(h+1) – 1 – (h + 1), or N – h – 1.
N = Number of nodes, h = Height of the tree
Have a look at the number of nodes at each layer in the perfect binary tree, shown in figure-10.
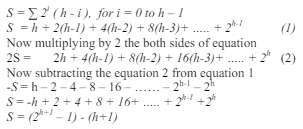
So, S is the sum of height. And it proves the theorem.
We can also write it like this:
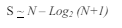
Proof of Theorem
- For any node in the tree that has some height h, darken h tree edges –Go down the tree by traversing left edge then only right edges.
- There are N – 1 tree edges, and h edges on right path, so number of darkened edges is N – 1 – h, which proves the theorem.
We’re going to implement these points step-by-step through figures.
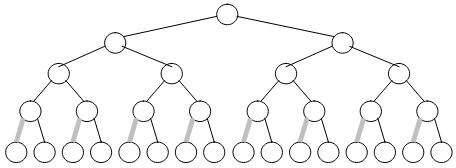
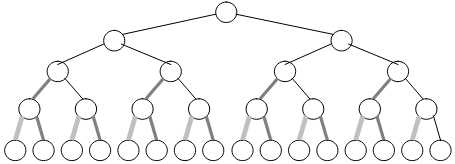
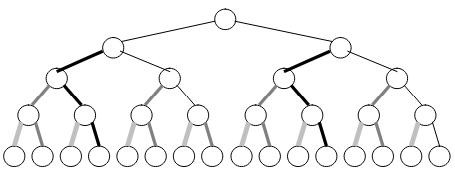
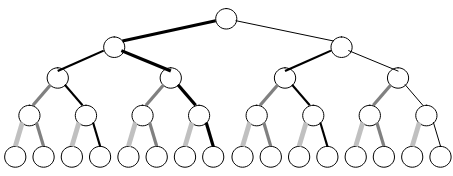
You’ll find that the number of darkened edges in figure-15 are exactly equal to the sum of heights ‘S’ of the binary tree.
For example, in the figures (12 to 15), we’ve: N=31, H=4. After putting these values in N-H-1 (31-4-1), we get 26. And 26 is the number of dark edges present in the binary tree.
REFERENCE: CS301 Handouts (page 355 to 378)








Dear Mam:
Assalam Alaikum:
First I found the Books Code CS301 Data Structure very difficult but since I got your website link it has very good information you have guided and everyone can understand it easily but now it is for me. It is very easy, I did the mid preparation from the same website and I am also doing the final preparation from the same website. I wish you well, I pray that Allah will make you successful in every step of your life.
Thanks Mam;
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.