Generating Maze using Disjoint Sets

Introduction

You might have seen puzzle game in any magazine. In which, you’ve to enter from one inlet and find a way out. If you’re asked to generate the maze daily, you can do this using disjoint data structure. In this article, we’ll discuss the examples of disjoint sets, including little concept of image segmentation and finally building the maze.

Maze example will have the procedure and algorithm that you’ll use in randomly generating the maze.

Image segmentation

Images are partitioned into small segments, where each segment acts as a pixel. Computer understands things through numbers. So, we assign each pixel a number ranging from 0 to 255. It can be greater than 255, depending upon the camera’s resolution.

In the color images, we store three colors i.e. RGB (Red, Green, Blue). By combining these three colors, new one can be obtained.

Let’s study black and white image.

• 0: white
• 255: black
• Between 0 to 255: gray

Idea behind the Image Segmentation

We’ll divide the image into different parts. An image may be segmented with regard to the intensity of the pixels. We may have groups of pixels having high intensity and those with pixels of low intensity. These pixels are divided on the basis of their threshold value. After this, these pixels will be grouped on the basis of threshold difference in intensity of neighbors.

Pictorial Example for Image Segmentation

Figure-1 is the small squares of black and white squares represent pixels. This is 5×5 image (5 rows, 5 columns). Let’s put 0 for white, 2 for gray, and 4 for black. Then, we get Figure-2:

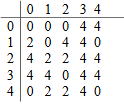
Now, we keep the threshold of 4. Means, put 1 for those that have values more than 4 and put 0 for pixels having less than 4. After doing this, we get Figure-3:

We’ll perform union operation i.e. making all the neighboring 1s as one set. Figure-4 shows that how the majority of 1s in a region are grouped, having threshold of 4.

Now, let’s change the threshold to 2 (if 2 or greater than 2, put 1 otherwise 0). We get Figure-5:

Figure-6 after performing union operation:

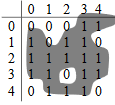
Union-find method doesn’t require much storage. Initially, we’ve 25 sets stored in the array and we do all the processing within the array without using any extra memory.

Generating Maze

Maze is helpful in robotics where robots looks for the path to enter any room. You can generate the random maze using the knowledge of disjoint sets and union-find algorithm. “Random” means that the system should generate a new maze every time.

Let’s take a 5×5 grid and generate 5×5 maze.

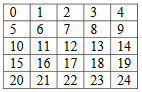
Figure-7 contains 25 cells, named 0 to 24. The walls isolate each cell from the others. Remove these walls randomly to establish a path from the first cell to the last cell.

This corresponds to an equivalence relation, meaning two cells are equivalent if they can be reached from each other, with walls removed so there is a path from one to the other. Means, if we remove the walls between two cells. Then, we’ve established an equivalence relationship between them.

First of all, we’ll decide the entrance and exit of the maze. Later, we’ll do the rest of job.

Algorithm for the Maze

• Randomly remove walls until the entrance and exit cells belong to the same set.
• Removal of the wall is the same as doing a union operation.
• Do not remove a randomly chosen wall if the cells it separates already belong to the same set.

We take cells randomly, which means that the probability of removing the wall of each cell is equal. Now, after removing a wall between 2 cells, we’ve combined these two cells into one set (union method).

At the end, the entrance and exit cells will belong to the same set.

The elements of the set will keep on growing and at some point, we may have the entrance cell (cell 0) and the exit cell (cell 24) in the same set. The entrance cell and the exit cell being in the same set indicates that the elements are related to each other, and no wall exists between them.

Pseudo Code of the Maze generation

We’ll use the entrance as 0 and exit as size-1 by default.

MakeMaze(int size) {
    entrance = 0; exit = size-1;
    while (find(entrance) != find(exit)) {
        cell1 = randomly chosen cell
        cell2 = randomly chosen adjacent cell
        if (find(cell1) != find(cell2) {
            knock down wall between cells
            union(cell1, cell2)
        }
    }
}

Pictorial View of generating the Maze

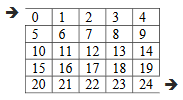
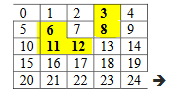
After deciding cell 0 as entrance and cell 24 as exit point, let’s choose cell 11 randomly.

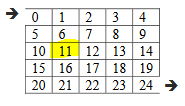
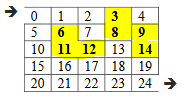
Now, randomly choose one of its walls, suppose we get the right wall. We’ll take cell 11 in the cell1 and cell 12 in cell2 variables. Find(cell 11) returns set_11 and find(cell 12) returns set_12. The union operation removes the wall between these two cells, as shown in Figure-10.

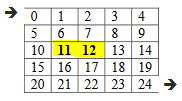
Now we can move from cell 11 to cell 12 and vice versa due to the symmetry condition of disjoint sets.

We’ve created a new set (set_11 = {11, 12} ).

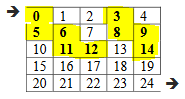
Now we randomly choose the cell 6 and its bottom wall. And we get Figure-11. In this, we get set_11 containing 3 elements: cell 11, cell 12, and cell 6.

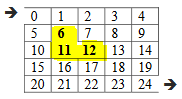
We’ll continue choosing the random cell and removing its random wall until we don’t make entrance and exit cells into one same set.

Try using this algorithm in your program. And don’t forget sharing your experience in the comment section. 😊

Conclusion

Disjoint sets help in image segmentation for image processing and generating maze for helping robots to find the path. Moreover, the union-find algorithm makes the disjoint set ADT known for its efficiency.

REFERENCE: CS301 Handouts (page 416 to 423)