Introduction
Huffman code is method for the compression of standard text documents. It makes use of a binary tree to develop codes of varying lengths for the letters used in the original message. Huffman code is also part of the JPEG image compression scheme. The algorithm was introduced by David Huffman in 1952 as part of a course assignment at MIT.
This article will guide you about how you can encode the data using Huffman encoding method.
Why Huffman Encoding?
Data compression plays a significant role in computer networks. To transmit data to its destination faster, it is necessary to either increase the data rate of the transmission media or simply send less data. The other way is to increase the bandwidth.
What happens?
We usually compress the file (using winzip) before sending. The receiver of the file decompresses the data before making its use.
Example of Encoding Data using Huffman Encoding
We’ll take a simple example to understand it. The example is to encode the 33-character phrase (including space):
“traversing threaded binary trees“
Importance of Huffman encoding in given scenario
- As every character is of 8 bits, therefore for 33 characters, we need 33 * 8 = 264.
- But the use of Huffman algorithm can help send the same message with only 116 bits. So we can save around 40% using the Huffman algorithm.
Algorithm for Huffman Encoding
- List all the letters used, including the “space” character, along with the frequency with which they occur in the message.
- Consider each of these (character, frequency) pairs to be nodes; they are actually leaf nodes, as we will see.
- Pick the two nodes with the lowest frequency. If there is a tie, pick randomly amongst those with equal frequencies.
- Make a new node out of these two, and turn two nodes into its children.
- This new node is assigned the sum of the frequencies of its children.
- Continue the process of combining the two nodes of lowest frequency till the time only one node, the root is left.
Implementation of the Algorithm for Huffman Encoding
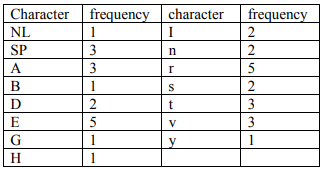
NL = New Line, SP = Space
Frequency = Number of times a character found in the data
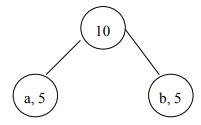
Suppose, in a file, the letter ‘a’ occurs 50 times and ‘b’ and ‘c’ five times each. Here, ‘b’ and ‘c’ have the lowest frequency. We will take these two letters as leaf nodes and build the tree from these ones. As fourth step states, we make a new node as the parent of these two nodes. The ‘b’ and ‘c’ are its children. In the fifth step, we assign to this new node the frequency equal to the sum of the frequencies of its children. Thus a three-node tree comes into existence. This is shown in the following figure.
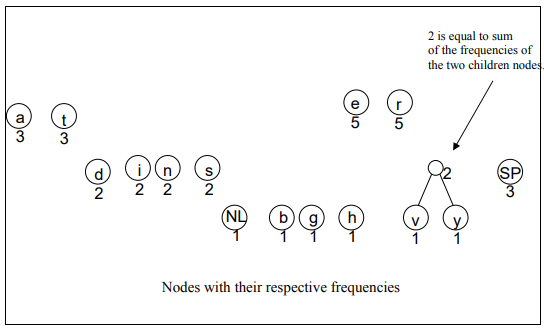
Now, keeping our given example in view, we can easily proceed the process of encoding. You would observe that how lower frequency nodes are being combined to make the parent node of combined frequencies of its children. And then they further combine to make another node. This process continues until we don’t get the parent node having frequency equal to the number of characters present in the data.
Following images are showing the logical activity, in real, computers don’t do that. 🙂
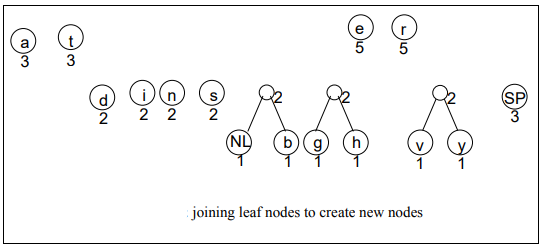
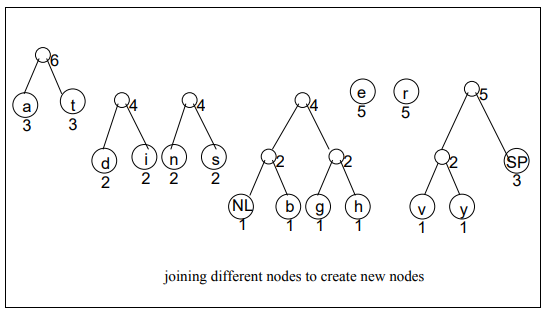
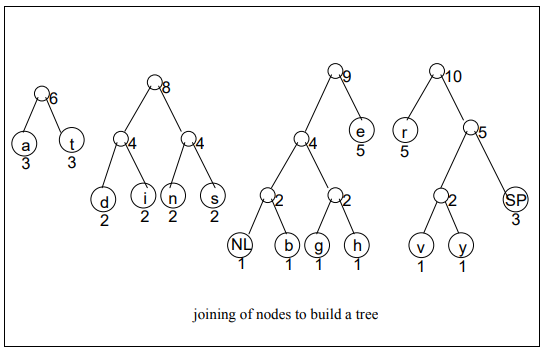
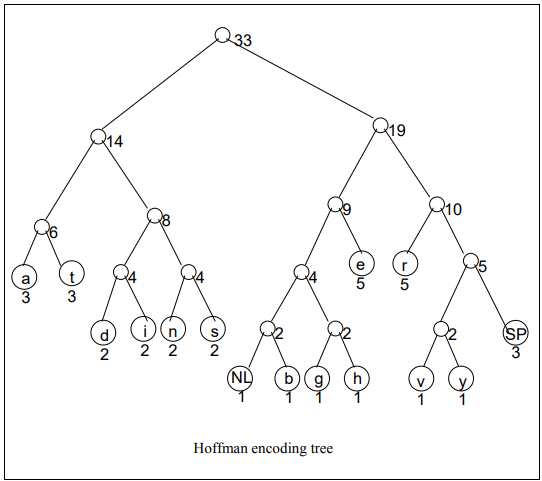
Finally Encoding the Data through Huffman Encoding
To go ahead, we have to do the following steps:
- Start at the root. Assign 0 to left branch and 1 to the right branch.
- Repeat the process down the left and right subtrees.
- To get the code for a character, traverse the tree from the root to the character leaf node and read off the 0 and 1 along the path.
You can see the implementation of 1st 2 steps in the following image:
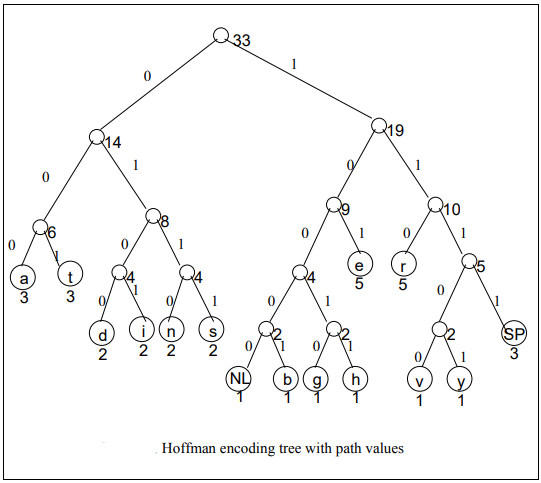
Now the journey from the root to the leaf node for every character is shown below (3rd step):
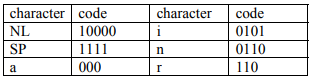

🎉Congratulations! The encoded form of the message is given in below image:

Conclusion of the given Example
- Original message: 8 bit per character, length was 264
- Message encoded using Huffman encoding: Compressed into 122 bits, 54% reduction.
One More Thing
We put the new node in the queue. It takes its position with respect to its frequency as we’re using the priority queue. It’s evident in procedure that we proceed to take two nodes from the queue. These are removed and their parent node goes back to the queue with a new frequency.
REFERENCE: CS301 Handouts (page 292 to 305)