Skip List _Efficiency in Linked List

Introduction

Search operation in the linked list is very slow. Because we’ve to pass through every element in the list, to find the element that we want. For this, we’ll use the skip list. In this article, we’ll talk about insertion and deletion in the skip list. And learn about quad node or doubly skip list.

Skip list

It performs jumps in the linked list instead passing through each and every element in the list to carry out fast search operation.

The main base of skip list is the linked list. Figure-1 shows the linked list that has a head and tail, and each pointer in node is pointing the element next to it.

Figure-2 shows the skip list.

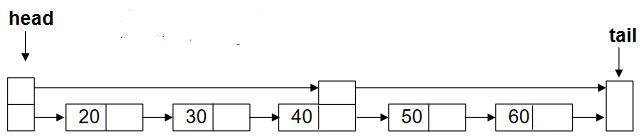
• The node in the middle has two next pointers; one is the old linked list leading to next node 50 and second is leading to the tail node.
• The “head” node also has two pointer. One is pointing to the old linked list (node 20) and second is pointing to the middle node (40).

Understand the algorithm through example.

• Let, we want to find “60” in the list.
• First, we’ll come to the middle through the second pointer of “head” node. And this middle element came out to be “40”.
• 40 is less than 60. Therefore, right half of the list is selected.

You can add additional pointers (links) and boost the performance.

Skip List of Higher Level Chains

• For general n, level 0 chain includes all elements.
• Level 1 every other element, level 2 chain every fourth, etc.
• Level i, every 2^i th element.

You can see that level 1 has link to every other node in the list. Level 2 links to every 4rth element in the list. We keep on adding new levels of chains to generalize level i. Level i will have link to every (2^i)th element.

Using this kind of skip list data structure, we can find elements in log(n) (log with base 2) time.

Problem: Frequency of pointers increases in the list. This makes insertion and deletion complex, as it becomes hard to readjust these pointers.

Professor Pugh suggested that instead of doing leveling in the power of 2, it should be done randomly.

Definition of Skip List

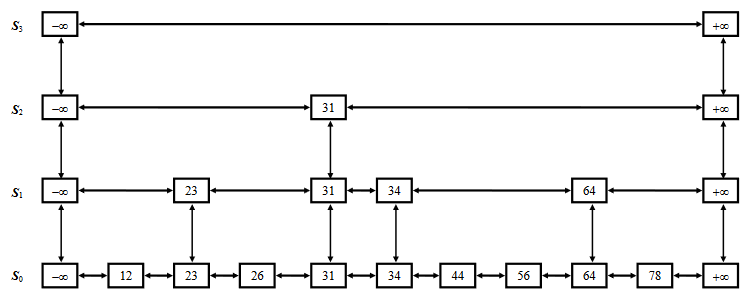
A skip list for a set S of distinct (key, element) items is a series of lists S0, S1 , … , Sh such that

• Each list Si contains the special keys +∞ and -∞.
• List S0 contains the keys of S in non-decreasing order.
• Each list is a subsequence of the previous one, i.e., S0 ⊇ S1 ⊇ … ⊇ Sh.
• List Sh contains only the two special keys.

The first and last nodes of S0 contain -∞ and +∞ respectively. In the computer, we can put these values by –max(int) and max(int). The values can also be used about which we are sure that these will not be in the data items.

The node should not be every other or fourth node. It will be a random selection.

We know from the third point; S1 is the subset of S0. So, we chosen 23, 31, 34, and 64 randomly for S1, shown in Figure-4.

S2 is the subset of S1. A pointer is added from -∞ to 31 and 31 to +∞. And S3 is the subset of S2.

Note: S1, S2, and S3 are the result of additional pointers. It’s not the duplication of data. Just multiple pointers are added to point at different elements for fast search operations. Example: node 23 exists once but has two next pointers. One is pointing to 26 while the other pointing to 31.

Skip List Search

We want to keep linked list structure. But do not want to search n elements for finding an item. We want to implement the algorithm like binary search on the linked list.

We search for a key x in the following fashion:

• We start at the first position of the top list.
• At the current position p, we compare x with y ← key(after(p)).
  • x = y: we return element(after(p)). x > y: we “scan forward”.
  • x < y: we “drop down”.
• If we try to drop down past the bottom list, we return NO_SUCH_KEY.

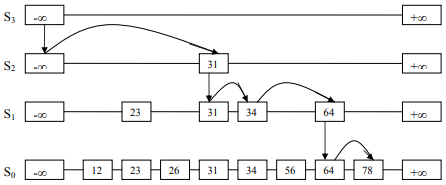
See Figure-5. Suppose, we want to find 78. We denote this current node 78 with p. Now, we look the node after p, which is +∞. And this is greater than 78. So, we drop down from S3 to S2. After this, we again look for the node next to it, which is 31. 31 is less than 78. So, we scan forward and again face +∞. Again, we drop down from S2 to S1. Then, reach 34. As 34 < 78, so scan forward. Faces 64<78, next is +∞. So, we drop down from this 64 of S1 to S0. Scan forward and find 78.

Now, speed of search operation in skip list has been increased.

Insertion in Skip List

When we are going to insert (add) an item (x,0) into a skip list, we use a randomized algorithm.

• We repeatedly toss a coin until we get tails, and we denote with i the number of times the coin came up heads.
• If i > h, we add to the skip list new lists Sh+1, … , Si +1, each containing only the two special keys.

Here we compare i (that is the count of heads came up) with h (that is the number of list) if i is greater than or equal to h then we add new lists to the skip list.

• We search for x in the skip list and find the positions p0, p1 , …, pi of the items with largest key less than x in each list S0, S1, … , Si.
• For j ← 0, …, i, we insert item (x, o) into list Sj after position p.

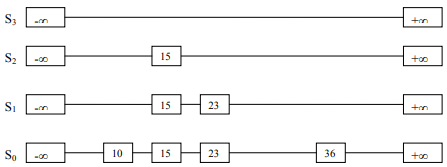
Have a look at Figure-6. We’ve a skip list of three elements: 10, 23, and 36. We want to add node 15 in it. We tossed the coin and found the head two times before the tail. On this, we stopped. So, i=2 (no. of tosses having head before we encountered tail). And h=2 (total heads).

As you see, i=h, we’re done here. Based on i=h, we’ll just have two more sets: S1 and S2. Now, let’s add 15 in the skip list. 15 is greater than -∞. So, jump down from -∞ of S2. Then, scans forward and faces 23 which is less than 15. Again, drop down from -∞ of S1 to S0. On S0, sees 10, and then 23. As 10<15<23. So, it’ll be fixed between 10 and 23.

See Figure-7.

We’ll not really toss the coin rather generate the random number, facility is available in C/C++ library.

Randomized Algorithm

• A randomized algorithm performs coin tosses (i.e., uses random bits) to control its execution.
• It contains statements of the type:

b ← random()
if b <= 0.5 // head
    do A …
else // tail
    do B …

• Its running time depends on the outcome of the coin tosses, i.e, head or tail.

Deletion from Skip List

Deletion method is performed by first finding the node, and then removing it. To remove a key x from the skip list, we proceed in the following way: We search for x in the skip list and find the positions p0, p1 , …, pi of the items with key x, where position pj is in list Sj.

We remove positions p0, p1 , …, pi from the lists S0, S1, … , Si. We remove all the lists except the list containing only the two special keys.

We see additional links in S1 and S2 for the node 23. When we perform traversal in search of 34, we label the links as p2, p1, and p0. Now, we remove the node 34 and change the pointers in the lists.

In short, we intend to remove the node and readjust the links.

We see the list S0, and have multiple links at the nodes 26, 40, and 57. These multiple links are looking like tower on these nodes. That’s why these nodes are called TowerNode. See Figure-10.

TowerNode will have an array of next pointers. Actual number of next pointers will be decided by the random procedure. We also need to define MAXLEVEL as an upper limit on number of levels in a node. We’ll allocate the next pointer space for TowerNode dynamically.

Node may have two pointers, one directing forward and the other directing backward.

Now, we’re going to discuss Quad Node. You might have got the idea this will make the navigation flexible. Let’s see:

Quad Node

In this, we’ve four next pointers. It’s also called doubly skip list.

The quad node stores:

• Item
• Link to the node before
• Link to the node after
• Link to the node below
• Link to the node above

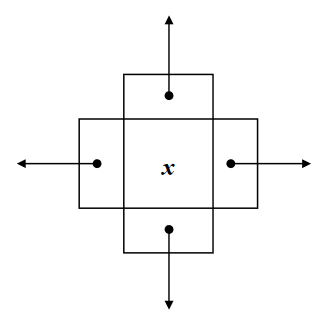
This will require copying of the key (item) at different levels. We do not have an array of next pointers in it. So different ways are adopted to create a multilevel node of skip list. While requiring six levels, we will have to create six such nodes and copy the data item x in all of these nodes and insert these in link list structure. The following figure depicts it well.

The advantage of using quad node is that we don’t have to allocate the space for next pointers.

Performance of Skip Lists

In a skip list, with n items the expected space used is proportional to n. It can’t be n^2 or n^3. The expected search, insertion and deletion time is proportional to log n.

Conclusion

In this data structure, we need not to go for rotations and balancing like AVL tree. In this data structure- Skip-list, we get rid of the limitation of arrays. This way, the search gets very fast. Moreover, we have sorted data and can get it in a sorted form.

REFERENCE: CS301 Handouts (Page 438 to 452)