Introduction
In this article, we’re going to study algorithms of sorting. Know that, we’re not talking about data structures. Because we use a data structure to contain a data and we use algorithms to perform certain operations or actions on that data. Here, we’ll emphasize on different types of sorting and the level of their efficiency. And also the approaches to implement those algorithms.
What is Sorting?
Sorting means to put the data in a certain order or sequence.
It is so useful that in 80-90% of computer applications, sorting is there in one form or the other.
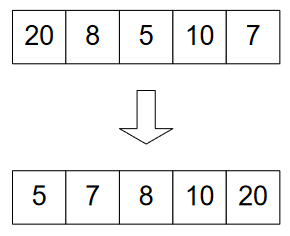
In Figure-1, you see unsorted numbers become sorted. It’s easy to sort it when there are less number of elements. But if you’re given millions of elements, then we need some efficient mechanism to perform this task.
Elementary Sorting Algorithms
- Selection Sort
- Insertion Sort
- Bubble Sort
These are elementary algorithms because they are very simple.
Selection Sort
Here is the main idea for this type of sort: –
- find the smallest element
- put it in the first position
- find the next smallest element in the remaining elements
- put it in the second position
- …
- And so on, until we get to the end of the array
Let’s understand it through an example: –
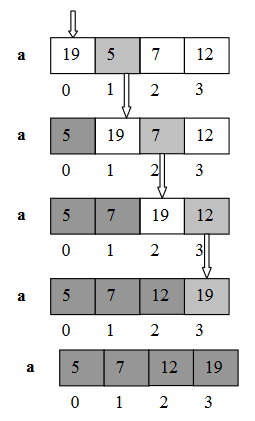
In Figure-2, the top array is un-sorted. First, we looked for the minimum number from that array which is “5”. Then, swapped it with the element at index 0. Second, we searched next part of the array for minimum number and then performed swapping. We’ll continue until the whole array don’t get sorted.
Selection Sort Algorithm in C++
void selectionSort(int *arr, int N){
int posmin, count, tmp;
for (count=0;count<N;count++){
posmin = findIndexMin(arr, count, N);
tmp=arr[posmin];
arr[posmin]=arr[count];
arr[count]=tmp;
}
}
int findIndexMin (int *arr, int start, int N){
int posmin=start;
int index;
for(index=start; index < N; index++)
if (arr[index]<arr[posmin])
posmin=index ;
return posmin ;
}In the given code, we sort the array in selectionSort(int *arr, int N) and find the minimum number in findIndexMin(int *arr, int start, int N).
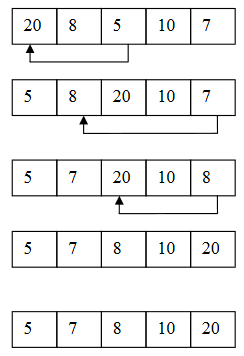
You can implement above code for given example in Figure-3.
Selection Sort Analysis
Time complexity of selection sort is proportional to N^2.
To find the first smallest element, we have to go through the N elements of the array. For the 2nd smallest element, we’ve to search N-1 elements. During this search process, we’ve to search two elements for the second last smallest element. And obviously in the end, there is one element that is at its proper position, necessitating no search. We have to do all these searches. These are N, N-1, N-2 ……2, 1 for the first, second, third ……second last and last element respectively. Number of total searches are equal to the sum of all these searches.
Total searches = 1 + 2 + 3 + …….+ (N-2) + (N-1) + N
= N (N+1) / 2
= (N^2 + N) / 2If N is 1 million, N^2 is going to be very large as compared to N. Thus, we can ignore N and can say that the total searches is proportional to N^2.
Insertion Sort
Main idea: –
- Start by considering the first two elements of the array data. If found out of order, swap them.
- Consider the third element; insert it into the proper position among the first three elements.
- Consider the fourth element; insert it into the proper position among the first four elements.
- … …
See Figure-4 to understand this sorting properly. We continue to take beginning elements and compare them. Based on their value, we sort them by performing swap.
Insertion Sort Algorithm in C++
void insertionSort(int *arr, int N){
int pos, count, val;
for(count=1; count < N; count++){
val = arr[count];
for(pos=count-1; pos >= 0; pos--)
if (arr[pos] > val)
arr[pos+1]=arr[pos];
else break;
arr[pos+1] = val;
}
}We have to shift the elements. This shifting is an additional overhead of this sorting algorithm. Due to this shifting, the sorting requires more time. This algorithm is also an in place algorithm as we don’t need any additional storage.
Value at current position = arr[pos]
We compare val and arr[pos]. If val is less than arr[pos], then its mean is that val has to go to the left of the arr[pos]. So, we shift arr[pos] to right to create place for the new value i.e val. When the loop exits, we put this value at arr[pos+1].
Insertion Sort Analysis
Insertion sort is an N^2 algorithm.
In the sort process, there may be a situation that every iteration inserts an element at the start of the array by shifting all sorted elements along. For placing the third element at the start position, we have to shift two elements. In the worst case, we may have to bring the element to the first place at every iteration.
After summing up all the shifting, the total becomes 2 + 3 + 4 +……. + N-1 + N.
Total = (2 + N ) (N -1) / 2
= O (N2 )When N increases, the value of N^2 will dominate.
Bubble Sort
If we consider the array as vertical, then we bring the smaller elements upward in the array step by step and as a result, the larger elements go downward.
Main idea: –
- Exchange neighboring items until the largest item reaches the end of the array.
- Repeat the above step for the rest of the array.
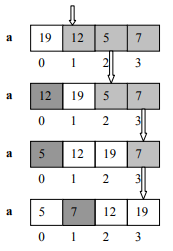
It can be well understood through an example. See Figure-5.
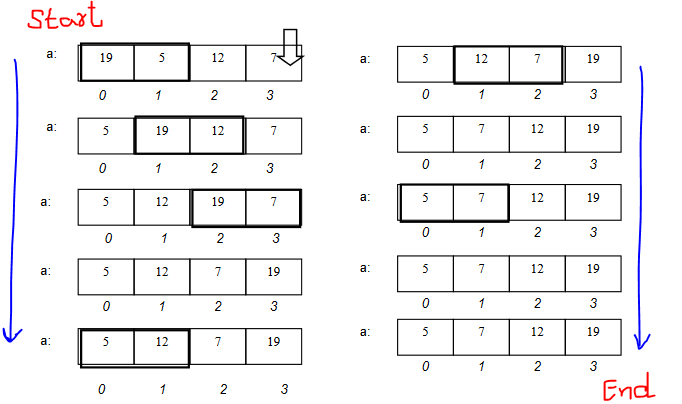
In Figure-5, first two elements are compared. Based on their value, we performed swapping. Second, we picked next two elements (2nd, 3rd) and performed swapping based on their values. If the one loop completes its job (whole array has been traversed), and our array is still not sorted. Then, we start the same procedure of comparison and swapping again. We continue performing this method until we’re not sure that whole array has been sorted.
To get the surety of sorted array, we’ll set the flag based on if we’ve swapped any of the pairs in a loop or not. In other words, flag will tell that swapping has been performed or not. If yes, then traverse the whole array otherwise no need of it, because it’s sorted.
Bubble Sort Algorithm in C++
void bubbleSort(int *arr, int N){
int i, temp, bound = N-1;
int swapped = 1;
while (swapped > 0 ){
swapped = 0;
for(i=0; i < bound; i++)
if ( arr[i] > arr[i+1] ){
temp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = temp;
swapped = i;
}
bound = swapped;
}
}The outer loop that is the while loop executes as long as swapping is being done. In the loop, we initialize the swapped variable with zero. When it is not changed in for loop, it means that the array is now in sorted form and we exit the loop.
Bubble Sort Analysis
The time complexity of this sorting technique increases proportional to N^2.
This sorting algorithm has two loop: outer and inner.
- Outer loop executes N times where it has to pass the whole array.
- Inner loop executes N times first, then for N-1, and then for N-2 times. So, this inner iteration’s range decreases with each of the iteration of the outer loop.
Now if we sum up these iterations i.e. 1 + 2 + 3 + ……… + N-1 + N. Then this summation becomes N (1 + N)/ 2 = O (N^2). When N increases too much, we ignore N and just rely on N^2.
Conclusion
These sorting methods are easy to understand and code. They take advantage in terms of storage where we don’t need extra space for sorting. But these algorithms are expensive with respect to time performance, where their time complexity is proportional to N^2.
But also we’ve other algorithms to overcome this time performance. Where we’ll be able to bring the time complexity proportional to: –
[latex]\[N{\log _2}(N)\][/latex]We’ll learn about these sorting methods for time optimization in the next articles.
REFERENCE: CS301 Handouts (page 472 to 483)







